题目内容
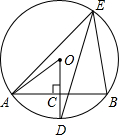
16. 如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$.
如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$.(1)求AB的长;
(2)连结BC和BD,请判断△BCD的形状,并证明.
分析 (1)连接OC,设OC=r,则OE=r-1,在Rt△OCE中,利用勾股定理求出r的值,进而可得出结论;
(2)根据(1)中AB的长得出BE的长,由锐角三角函数的定义得出∠BCD的度数,进而可得出∠BDC的度数,由此可得出结论.
解答  解:(1)连接OC,设OC=r,则OE=r-1,
解:(1)连接OC,设OC=r,则OE=r-1,
∵⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$,
CE=DE=$\sqrt{3}$.
在Rt△OCE中,
∵CE2+OE2=OC2,即($\sqrt{3}$)2+(r-1)2=r2,解得r=2,
∵AB=2r=4;
(2)△BCD是等边三角形.
理由:∵AB=4,AE=1,
∴BE=4-1=3,
∴tan∠BCD=$\frac{BE}{CE}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴∠BCD=60°.
∵AB⊥CD,
∴∠BDC=∠BCD=60°,
∴△BCD是等边三角形.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
7.计算(3.5×103)×(2.2×105)的结果并用科学记数法表示,正确的结果是( )
| A. | 770000000 | B. | 77×107 | C. | 7.7×108 | D. | 7.7×107 |
1.如图,已知方格纸中有A、B、C三个格点,求作一个以A、B、C为顶点的格点四边形.
(1)在图1中作出的四边形是中心对称图形但不是轴对称图形.
(2)在图2中作出的四边形是轴对称图形但不是中心对称图形.
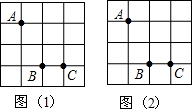
(1)在图1中作出的四边形是中心对称图形但不是轴对称图形.
(2)在图2中作出的四边形是轴对称图形但不是中心对称图形.

2.a与b是两个连续整数,若a<$\sqrt{7}$<b,则a,b分别是( )
| A. | 6,8 | B. | 3,2 | C. | 2,3 | D. | 3,4 |
 如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.
如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数. 如图,六边形ABCDEF中,AF=CD,AB=DE,FE=BC,∠B=∠E,求证:AF∥CD.
如图,六边形ABCDEF中,AF=CD,AB=DE,FE=BC,∠B=∠E,求证:AF∥CD. 如图,在平面直角坐标中,点A的坐标为(4,0),直线AB⊥x轴,直线y=-$\frac{1}{4}$x+3经过点B,与y轴交于点C.
如图,在平面直角坐标中,点A的坐标为(4,0),直线AB⊥x轴,直线y=-$\frac{1}{4}$x+3经过点B,与y轴交于点C.