题目内容
6.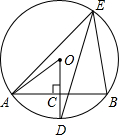 如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.
如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.
分析 先根据圆心角、弧、弦的关系得出$\widehat{AD}$=$\widehat{BD}$,AB⊥OD,故可得出∠DEB=$\frac{1}{2}$∠AOD,由直角三角形的性质求出∠AOD的度数即可.
解答 解:∵点D是弧AB的中点,
∴$\widehat{AD}$=$\widehat{BD}$,AB⊥OD,
∴∠DEB=$\frac{1}{2}$∠AOD.
∵∠OAC=40°,
∴∠AOD=90°-40°=50°,
∴∠DEB=$\frac{1}{2}$∠AOD=25°.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
1.为了了解全校七年级439名学生的视力情况,骆老师从中抽查了45名学生的视力情况.针对这个问题,下面说法正确的是( )
| A. | 439名学生是总体 | B. | 每名学生是个体 | ||
| C. | 这个样本容量是45 | D. | 45名学生是所抽取的一个样本 |
 列方程解应用题:
列方程解应用题: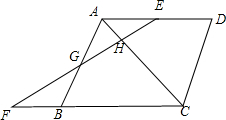 如图,在菱形ABCD中,E是AD的中点,EF⊥AC,交AB于G,交CB延长线于F.求证:GE=GF.
如图,在菱形ABCD中,E是AD的中点,EF⊥AC,交AB于G,交CB延长线于F.求证:GE=GF. 如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$.
如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$.