题目内容
11. 如图,在平面直角坐标中,点A的坐标为(4,0),直线AB⊥x轴,直线y=-$\frac{1}{4}$x+3经过点B,与y轴交于点C.
如图,在平面直角坐标中,点A的坐标为(4,0),直线AB⊥x轴,直线y=-$\frac{1}{4}$x+3经过点B,与y轴交于点C.(1)求点B的坐标;
(2)直线l经过点C,与直线AB交于点D,E是直线AB上一点,且∠ECD=∠OCD,CE=5,求直线l的解析式.
分析 (1)根据点A的坐标结合AB⊥x轴可得出直线AB的解析式,进而可得出点B的横坐标,再结合一次函数图象上点的坐标特征即可得出点B的坐标;
(2)令直线AD与x轴的交点为点M,根据平行线的性质可得出∠MDA=∠DCO,结合∠ECD=∠OCD即可得出CE=DE,设点E的坐标为(4,m),则点D的坐标为(4,m-5),根据一次函数图象上点的坐标特征可得出点C的坐标,结合CE=5利用两点间的距离公式即可得出关于m的方程,解方程即可得出m的值,将其代入点D的坐标中可得出点D的坐标,再根据点C、D的坐标利用待定系数法即可求出直线l的解析式.
解答 解:(1)∵点A的坐标为(4,0),直线AB⊥x轴,
∴直线AB的解析式为x=4.
当x=4时,y=-$\frac{1}{4}$×4+3=2,
∴点B的坐标为(4,2).
(2)令直线AD与x轴的交点为点M,如图所示.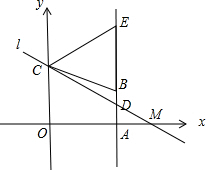
∵AB⊥x轴,CO⊥x轴,
∴AB∥CO,
∴∠MDA=∠DCO.
∵∠MDA=CDE,∠OCD=EDC,
∴∠CDE=∠DCE,
∴DE=CE=5.
当x=0时,y=3,
∴点C的坐标为(0,3).
设点E的坐标为(4,m),则点D的坐标为(4,m-5),
,∵CE=$\sqrt{(4-0)^{2}+(m-3)^{2}}$=5,
∴m1=6,m2=0,
∴点D的坐标为(4,1)或(4,-5).
设直线l的解析式为y=kx+3,
∴1=4k+3或-5=4k+3,
解得:k=-$\frac{1}{2}$或k=-2,
∴直线l的解析式为y=-$\frac{1}{2}$+3或y=-2x+3.
点评 本题考查了一次函数图象上点的坐标特征、待定系数法求函数解析式、平行线的性质以及等腰三角形的判定与性质,解题的关键是找出CE=DE=5.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
1.为了了解全校七年级439名学生的视力情况,骆老师从中抽查了45名学生的视力情况.针对这个问题,下面说法正确的是( )
| A. | 439名学生是总体 | B. | 每名学生是个体 | ||
| C. | 这个样本容量是45 | D. | 45名学生是所抽取的一个样本 |
3.化简:
| (1)$\sqrt{72}$; | (2)$\sqrt{48}$; | (3)$\sqrt{\frac{2}{3}}$; |
| (4)-2$\sqrt{\frac{9}{2}}$; | (5)$\sqrt{{a}^{3}b}$(a≤0); | (6)$\sqrt{{a}^{4}+2{a}^{2}{b}^{2}+{b}^{4}}$. |
 在一次高尔夫球的联赛中,高欣在距球洞10m处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{b}{5}$x,其中y(m)是球的飞行高度,x(m)是球飞行的水平距离,结果球落地离球洞的水平距离还有2m.
在一次高尔夫球的联赛中,高欣在距球洞10m处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{b}{5}$x,其中y(m)是球的飞行高度,x(m)是球飞行的水平距离,结果球落地离球洞的水平距离还有2m.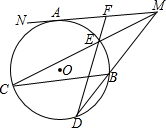 己知:⊙O与直线MN相切于A点,弦BC∥MN,直线MB与⊙O相交于D点,MC与⊙O相交于E,DE的延长线交MN于F点.求证:AF=FM.
己知:⊙O与直线MN相切于A点,弦BC∥MN,直线MB与⊙O相交于D点,MC与⊙O相交于E,DE的延长线交MN于F点.求证:AF=FM. 如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$.
如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$.