题目内容
2. 两个同心圆的半径分别为2cm和3cm,大圆弦AB与小圆相切,则AB=2$\sqrt{5}$cm.
两个同心圆的半径分别为2cm和3cm,大圆弦AB与小圆相切,则AB=2$\sqrt{5}$cm.
分析 连接OC和OB,根据切线的性质:圆的切线垂直于过切点的半径,知OC⊥AB,应用勾股定理可将BC的长求出,从而求出AB的长.
解答 解:连接OC和OB. ∵弦AB与小圆相切,
∵弦AB与小圆相切,
∴OC⊥AB,
在Rt△OBC中,
BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$.
∴AB=2BC=2$\sqrt{5}$.
点评 此题考查了切线的性质,勾股定理,以及垂径定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
12.实数$\sqrt{9}$的平方根( )
| A. | 3 | B. | -3 | C. | ±3 | D. | ±$\sqrt{3}$ |
10.已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数y=ax2+bx+c的图象上,则下列结论正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y1<y3 |
1.在Rt△ABC与Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠B',AB=A'B',则下面结论正确的是( )
| A. | AB=A'C' | B. | BC=B'C' | C. | AC=B'C' | D. | ∠A=∠A' |

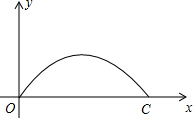 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和24秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需32秒.
如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和24秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需32秒.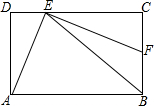 如图,在矩形ABCD中,BE平分∠ABC且交CD于点E,EF⊥AE且交BC于点F,求证:AE=EF.
如图,在矩形ABCD中,BE平分∠ABC且交CD于点E,EF⊥AE且交BC于点F,求证:AE=EF.