题目内容
1.在Rt△ABC与Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠B',AB=A'B',则下面结论正确的是( )| A. | AB=A'C' | B. | BC=B'C' | C. | AC=B'C' | D. | ∠A=∠A' |
分析 由AAS证明△ABC≌△A'B'C',即可得出结论.
解答 解:在△ABC与△A'B'C'中,$\left\{\begin{array}{l}{∠C=∠C'}&{\;}\\{∠A=∠B'}&{\;}\\{AB=A'B'}&{\;}\end{array}\right.$,
∴△ABC≌△A'B'C'(AAS),
∴∠B=∠A',AC=B'C',BC=A'C';
故选:C.
点评 本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定与性质是解决问题的关键,注意边或角的对应.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
16.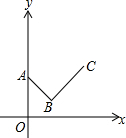 如图,某个函数的图象由线段AB和BC组成,其中点A(0,1.1),B(1,0.5),C(2,1.3),则此函数的最小值是( )
如图,某个函数的图象由线段AB和BC组成,其中点A(0,1.1),B(1,0.5),C(2,1.3),则此函数的最小值是( )
 如图,某个函数的图象由线段AB和BC组成,其中点A(0,1.1),B(1,0.5),C(2,1.3),则此函数的最小值是( )
如图,某个函数的图象由线段AB和BC组成,其中点A(0,1.1),B(1,0.5),C(2,1.3),则此函数的最小值是( )| A. | 0 | B. | 1.1 | C. | 0.5 | D. | 1.3 |
6.四个各不相等的整数a、b、c、d,满足abcd=9,则a+b+c+d=( )
| A. | 无法确定 | B. | 4 | C. | 10 | D. | 0 |
 两个同心圆的半径分别为2cm和3cm,大圆弦AB与小圆相切,则AB=2$\sqrt{5}$cm.
两个同心圆的半径分别为2cm和3cm,大圆弦AB与小圆相切,则AB=2$\sqrt{5}$cm. 等腰直角三角形ABC,∠ABC=90°,AB=2,O为AC中点,∠EOF=45°,求△BEF的周长.
等腰直角三角形ABC,∠ABC=90°,AB=2,O为AC中点,∠EOF=45°,求△BEF的周长. 在数轴上表示下列各数,并按从小到大的顺序用“<”把这些数连接起来.
在数轴上表示下列各数,并按从小到大的顺序用“<”把这些数连接起来.