题目内容
7. 如图,在平面直角坐标系中,函数y=2x-3和y=kx+b的图象交于点P(m,1),则关于x的不等式2x-3>kx+b的解集是x>2.
如图,在平面直角坐标系中,函数y=2x-3和y=kx+b的图象交于点P(m,1),则关于x的不等式2x-3>kx+b的解集是x>2.
分析 先利用一次函数图象上点的坐标特征确定P点坐标,然后写出直线y=2x-3在直线y=kx+b上方所对应的自变量的范围即可.
解答 解:把P(m,1)代入y=2x-3得2m-3=1,解得m=2,即P点(2,1),
当x>2时,2x-3>kx+b,
即不等式2x-3>kx+b的解集为x>2.
故答案为x>2.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知y=$\sqrt{x-3}$+$\sqrt{3-x}$+2,则xy的值为( )
| A. | 9 | B. | 8 | C. | 2 | D. | 3 |
19.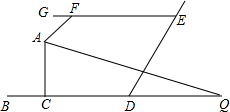 如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
 如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )| A. | 90° | B. | 95° | C. | 100° | D. | 105° |
17.6÷(-3)的值是( )
| A. | -2 | B. | 2 | C. | 3 | D. | -18 |
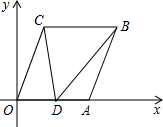 如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.