题目内容
16.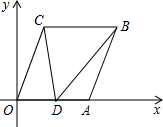 如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
分析 (1)由点的坐标的特点,确定出FC=2,OF=6,得出C(2,6);
(2)分点D在线段OA和在OA延长线两种情况进行计算;
(3)分点D在线段OA上时,α+β=θ和在OA延长线α-β=θ两种情况进行计算;
解答 解:(1)如图1,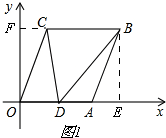
∵A(6,0),B(8,6),
∴FC=AE=8-6=2,OF=BE=6
∴C(2,6);
(2)设D(x,0),当△ODC的面积是△ABD的面积的3倍时,
若点D在线段OA上,
∵OD=3AD,
∴$\frac{1}{2}$×6x=3×$\frac{1}{2}$×6(6-x),
∴x=$\frac{9}{2}$,
∴D($\frac{9}{2}$,0);
若点D在线段OA延长线上,
∵OD=3AD,
∴$\frac{1}{2}$×6x=3×$\frac{1}{2}$×6(x-6),
∴x=9,
∴D(9,0)
(3)如图2.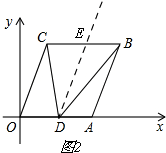
过点D作DE∥OC,
由平移的性质知OC∥AB.
∴OC∥AB∥DE.
∴∠OCD=∠CDE,∠EDB=∠DBA.
若点D在线段OA上,
∠CDB=∠CDE+∠EDB=∠OCD+∠DBA,
即α+β=θ;
若点D在线段OA延长线上,
∠CDB=∠CDE-∠EDB=∠OCD-∠DBA,
即α-β=θ.
点评 此题是几何变换综合题,主要考查了点三角形面积的计算方法,平移得性质,平行线的性质和判定,解本题的关键是分点D在线段OA上,和OA延长线上两种情况.

练习册系列答案
相关题目
4. 如图,将长方体表面展开,下列选项中错误的是( )
如图,将长方体表面展开,下列选项中错误的是( )
 如图,将长方体表面展开,下列选项中错误的是( )
如图,将长方体表面展开,下列选项中错误的是( )| A. |  | B. |  | C. |  | D. |  |
1.方程x2+4x-$\frac{10}{x}$+1=0的正数根的取值范围是( )
| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | 3<x<4 |
8.在下列各式中,计算正确的是( )
| A. | (2$\sqrt{3}$)2=6 | B. | $\sqrt{9}$=±3 | C. | $\sqrt{(-6)^2}$=-6 | D. | $\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$ |
6.下列多项式中,在有理数范围内不能用平方差公式分解的是( )
| A. | -x2+y2 | B. | 4a2-(a+b)2 | C. | a2-8b2 | D. | x2y2-1 |
 如图,在平面直角坐标系中,函数y=2x-3和y=kx+b的图象交于点P(m,1),则关于x的不等式2x-3>kx+b的解集是x>2.
如图,在平面直角坐标系中,函数y=2x-3和y=kx+b的图象交于点P(m,1),则关于x的不等式2x-3>kx+b的解集是x>2.