题目内容
2.化简(1)(-$\frac{2}{3}$xy2)-1÷($\frac{3z}{xy}$)2;
(2)$\frac{{{x^2}-2x+1}}{{1-{x^2}}}$.
分析 (1)直接利用负整数指数幂的性质结合分式除法运算法则化简求出答案;
(2)直接将分子与分母分解因式进而化简求出答案.
解答 解:(1)(-$\frac{2}{3}$xy2)-1÷($\frac{3z}{xy}$)2
=-$\frac{3}{2}$x-1y-2÷$\frac{9{z}^{2}}{{x}^{2}{y}^{2}}$
=-$\frac{3}{2}$x-1y-2×$\frac{{x}^{2}{y}^{2}}{9{z}^{2}}$
=$-\frac{x}{{6{z^2}}}$;
(2)$\frac{{{x^2}-2x+1}}{{1-{x^2}}}$
=$\frac{(1-x)^{2}}{(1-x)(1+x)}$
=$-\frac{x-1}{x+1}$.
点评 此题主要考查了分式的乘除运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
17.若${\sqrt{a^2}^{\;}}$=3,则a的值是( )
| A. | 3或-3 | B. | 3 | C. | -3 | D. | 9 |
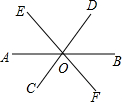 直线AB,CD,EF相交于点O,如图.
直线AB,CD,EF相交于点O,如图. 如图,在平面直角坐标系中,函数y=2x-3和y=kx+b的图象交于点P(m,1),则关于x的不等式2x-3>kx+b的解集是x>2.
如图,在平面直角坐标系中,函数y=2x-3和y=kx+b的图象交于点P(m,1),则关于x的不等式2x-3>kx+b的解集是x>2.