Question

19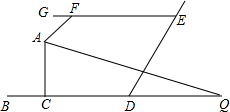．如图，BD∥GE，AQ平分∠FAC，交BD于Q，∠GFA=50°，∠Q=25°，则∠ACB的度数（　　）

• A． 90°
• B． 95°
• C． 100°
• D． 105°

Answer 1

分析 过点A作AH∥BD，由BD∥GE可知BD∥GE∥AH，由平行线的性质即可得出∠HAQ的度数，再由角平分线的定义即可求出∠QAC的度数，根据三角形外角的性质即可得出结论．

解答 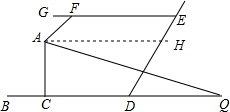解：过点A作AH∥BD，
∵BD∥GE，
∴BD∥GE∥AH，
∵∠GFA=50°，∠Q=25°，
∴∠FAH=50°，∠HAQ=∠Q=25°，
∴∠FAQ=∠FAH+∠HAQ=50°+25°=75°．
∵AQ平分∠FAC，
∴∠FAQ=∠CAQ=75°，
∵∠ACB是△ACQ的外角，
∴∠ACB=∠CAQ+∠Q=75°+25°=100°．
故选C．

点评 本题考查的是平行线的性质，根据题意作出平行线，利用平行线的性质求解是解答此题的关键．