题目内容
14.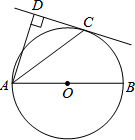 如图,AB是⊙O的直径,C是⊙O上一点,AD垂直与过点C的直线,垂足为D,AC平分∠BAD.
如图,AB是⊙O的直径,C是⊙O上一点,AD垂直与过点C的直线,垂足为D,AC平分∠BAD.(1)求证:CD是⊙O的切线;
(2)连接BC,若⊙O的半径为3,BC=2$\sqrt{3}$,求$\frac{AD}{DC}$的值.
分析 (1)连结OC,如图,由AC平分∠BAD得到∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,由于AD⊥CD,所以OC⊥CD,则可根据切线的判定定理得到CD是⊙O的切线;
(2)根据圆周角定理得到∠ACB=90°,则利用勾股定理可计算出AC=2$\sqrt{6}$,再证明Rt△ADC∽Rt△ACD,利用相似比得到$\frac{AD}{AC}$=$\frac{CD}{BC}$,然后利用比例的性质求解.
解答 (1)证明:连结OC,如图,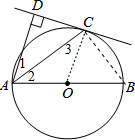
∵AC平分∠BAD,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ACB中,∵AB=6,BC=2$\sqrt{3}$,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{6}$,
∵∠1=∠2,
∴Rt△ADC∽Rt△ACD,
∴$\frac{AD}{AC}$=$\frac{CD}{BC}$,
∴$\frac{AD}{CD}$=$\frac{AC}{BC}$=$\frac{2\sqrt{6}}{2\sqrt{3}}$=$\sqrt{2}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了平行线的性质和相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 把一个含有45°角的三角板放在如图所示的两平行线上,测得∠α=120°,则∠β的度数为75°.
把一个含有45°角的三角板放在如图所示的两平行线上,测得∠α=120°,则∠β的度数为75°.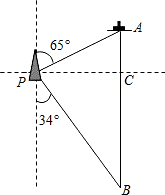 如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)
如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)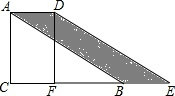 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于8,则平移距离等于( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于8,则平移距离等于( )