题目内容
13.已知圆内接四边形ABCD,且$\widehat{AB}$的度数:$\widehat{BC}$的度数:$\widehat{CD}$的度数:$\widehat{DA}$的度数为1:2:3:4,则∠A:∠B:∠C:∠D等于( )| A. | 1:2:3:4 | B. | 4:3:2:1 | C. | 4:3:1:2 | D. | 5:7:5:3 |
分析 根据题意画出图形,由弧度比等于角度比即可得出结论.
解答  解:如图所示,
解:如图所示,
∵且$\widehat{AB}$的度数:$\widehat{BC}$的度数:$\widehat{CD}$的度数:$\widehat{DA}$的度数为1:2:3:4,
∴设$\widehat{AB}$=x,则$\widehat{BC}$=2x,$\widehat{CD}$=3x,$\widehat{DA}$=4x.
∵弧度比等于角度比,
∴∠A=2x+3x=5x,∠B=3x+4x=7x,∠C=x+4x=5x,∠D=x+2x=3x,
∴∠A:∠B:∠C:∠D=5:7:5:3.
故选D.
点评 本题考查的是圆内接四边形的性质,熟知弧度比等于角度比是解答此题的关键.

练习册系列答案
相关题目
3.下列调查中,适合用普查方式的是( )
| A. | 了解某班学生“50米跑”的成绩 | |
| B. | 了解一批袋装食品是否含有防腐剂 | |
| C. | 了解江苏卫视“非诚勿扰”节目的收视率 | |
| D. | 了解一批灯泡的使用寿命 |
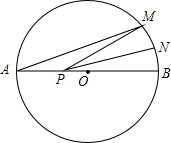 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为5.
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为5. 如图,在△ABC中,点D是BC的中点,FD⊥ED,延长ED到点P.使ED=PD,连结FP与CP,试判断BE+CF与EF的大小关系.
如图,在△ABC中,点D是BC的中点,FD⊥ED,延长ED到点P.使ED=PD,连结FP与CP,试判断BE+CF与EF的大小关系.