题目内容
4.如图1,⊙O的直径AB=4厘米,点C在⊙O上,设∠ABC的度数为x(单位:度,0<x<90),优弧$\widehat{ABC}$的弧长与劣弧$\widehat{AC}$的弧长的差设为y(单位:厘米),图2表示y与x的函数关系,则α=22.5度.
分析 直接利用弧长公式表示出y与x之间的关系,进而代入(a,3π)求出答案.
解答 解:设∠ABC的度数为x,根据题意可得:
y=$\frac{(360-2x)π×2}{180}$-$\frac{2xπ×2}{180}$
将(a,3π)代入得:
3π=$\frac{(360-2α-2α)×π×2}{180}$,
解得:α=22.5°.
故答案为:22.5.
点评 此题主要考查了动点问题的函数图象,正确得出y与x之间的关系式是解题关键.

练习册系列答案
相关题目
12.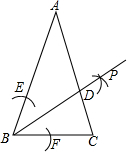 如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于$\frac{1}{2}$EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于$\frac{1}{2}$EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
 如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于$\frac{1}{2}$EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于$\frac{1}{2}$EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.| A. | 65 | B. | 75 | C. | 80 | D. | 85 |
19.下列运算中,正确的是( )
| A. | (a2)3=a5 | B. | a2•a4=a6 | C. | 3a2÷2a=a | D. | (2a)2=2a2 |
13.已知菱形的周长为20,它的一条对角线长为6,则菱形的面积是( )
| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
 如图,在Rt△ABC中,∠B=90°,AB<BC,分别以顶点A、C为圆心,以大于$\frac{1}{2}$AC长为半径作圆弧,两弧交于点MN,作直线MN,交边BC于点D,若BD=6,CD=10,则AB的长为8.
如图,在Rt△ABC中,∠B=90°,AB<BC,分别以顶点A、C为圆心,以大于$\frac{1}{2}$AC长为半径作圆弧,两弧交于点MN,作直线MN,交边BC于点D,若BD=6,CD=10,则AB的长为8. 如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$.
如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$.