题目内容
5.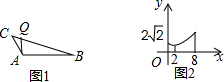 如图1,在钝角△ABC中,点Q从点C开始出发向点B运动,在运动过程中,设线段CQ的长为x,线段AQ的长为y,y关于x的函数图象如图2所示,横坐标为2时,是函数图象的最低点,则下列说法不正确的是( )
如图1,在钝角△ABC中,点Q从点C开始出发向点B运动,在运动过程中,设线段CQ的长为x,线段AQ的长为y,y关于x的函数图象如图2所示,横坐标为2时,是函数图象的最低点,则下列说法不正确的是( )| A. | ∠C的度数为45° | B. | AQ的最小值为2 | C. | △ABC的面积为8 | D. | sinB的值为$\frac{1}{3}$ |
分析 作AP⊥BC,由图象可知AC=2$\sqrt{2}$、AP=2可判断A、B选项,根据BC=8、AP=2可判断C选项,RT△ABP中BP=6、AP=2可判断D选项,
解答 解:由图象可知,当x=0时y=2$\sqrt{2}$,即AC=2$\sqrt{2}$,
如图作AP⊥BC,垂足为P,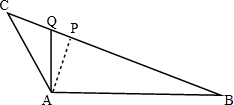
当点Q运动到点P位置时,AQ最小,由图象可知,其最小值为2,故B正确;
由AQ⊥AB时AQ=AP=2,可得在RT△ACP中,AC=2$\sqrt{2}$,AP=2,
∴sinC=$\frac{AQ}{AC}=\frac{2}{2\sqrt{2}}=\frac{\sqrt{2}}{2}$,
∴∠C=45°,故A正确;
∵由图象可知,BC=8,且根据以上可知BC边上的高AP=2,
∴S△ABC=$\frac{1}{2}$×8×2=8,故C正确;
在RT△ABP中,∵BC=8,PC=AP=2,
∴BP=6,
∴tanB=$\frac{AP}{BP}=\frac{1}{3}$,故D不正确;
故选:D.
点评 本题主要考查动点问题的函数图象,结合点的运动过程弄清函数图象上特殊点的数值的实际意义是解题的关键.

练习册系列答案
相关题目
4.如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的三倍,则称这样的方程为“3倍根方程”,以下说法不正确的是( )
| A. | 方程x2-4x+3=0是3倍根方程 | |
| B. | 若关于x的方程(x-3)(mx+n)=0是3倍根方程,则m+n=0 | |
| C. | 若m+n=0且m≠0,则关于x的方程(x-3)(mx+n)=0是3倍根方程 | |
| D. | 若3m+n=0且m≠0,则关于x的方程x2+(m-n)x-mn=0是3倍根方程 |
2.皖星书店年初以每本20元的价格购进一批畅销书《莫言精品集》,销售过程中发现,每月销售量y(本)与销售单价x(元)之间的关系如表所示,按照表中y与x的关系规律,解决下面的问题:
(1)试求出y与x的函数关系式.
(2)销售单价在什么范围时,书店能盈利?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)
| x | 25 | 28 | 30 | 32 | 35 |
| y | 250 | 220 | 200 | 180 | 150 |
(2)销售单价在什么范围时,书店能盈利?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)
10.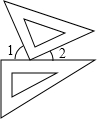 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠1=( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠1=( )
 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠1=( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠1=( )| A. | 72° | B. | 70° | C. | 54° | D. | 18° |
17. 如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
 如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )| A. | a>0,b<0,c>0 | B. | 当-1<x<2时,y>0 | ||
| C. | b2-4ac<0 | D. | 当x<$\frac{1}{2}$时,y随x的增大而减小 |
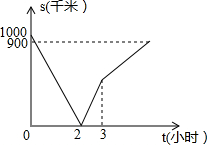 甲、乙、丙三地在一条直线上,乙地在甲地和丙地之间,一列高速列车从甲地开往乙地,一列快速列车从丙地经乙地开往甲地,两列列车同时出发,匀速行驶,且到达各自目的地后停止运行,从两列列车出发开始,至快速列车到达甲地为止,两列列车的距离s(千米)与行驶时间t(小时)之间的函数图象如图所示
甲、乙、丙三地在一条直线上,乙地在甲地和丙地之间,一列高速列车从甲地开往乙地,一列快速列车从丙地经乙地开往甲地,两列列车同时出发,匀速行驶,且到达各自目的地后停止运行,从两列列车出发开始,至快速列车到达甲地为止,两列列车的距离s(千米)与行驶时间t(小时)之间的函数图象如图所示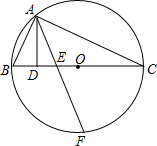 如图,△ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,连接OA,
如图,△ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,连接OA,