题目内容
5.在一次同学聚会上,若每两人握一次手,一共握了45次手,则参加这次聚会的同学一共有10名.分析 设这次参加聚会的同学有x人,已知见面时两两握手一次,那么每人应握(x-1)次手,所以x人共握手$\frac{1}{2}$x(x-1)次,又知共握手45次,以握手总次数作为等量关系,列出方程求解.
解答 解:设这次参加聚会的同学有x人,则每人应握(x-1)次手,由题意得:
$\frac{1}{2}$x(x-1)=45,
即:x2-x-90=0,
解得:x1=10,x2=-9(不符合题意舍去)
故参加这次聚会的同学共有10人.
故答案是:10.
点评 本题主要考查一元二次方程的应用,关键在于理解清楚题意,找出等量关系,列出方程求解.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
15.下列运算正确的是( )
| A. | ($\frac{a}{b}$)3=$\frac{{a}^{3}}{b}$ | B. | 3a3•2a2=6a6 | C. | 4a6÷2a2=2a3 | D. | (3a2)3=27a6 |
16.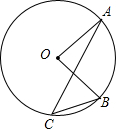 如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )
如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )
 如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )
如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )| A. | 30° | B. | 50° | C. | 60° | D. | 70° |
13.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛,在最近的10次选拔赛中,这两个人的跳远成绩(单位:cm)如图所示,请根据图中信息,解答下列问题:

(1)通过计算,补充完成下面的统计分析表.
(2)请依据对上述统计信息的数据分析,说明这两名运动员的成绩各有什么特点?

(1)通过计算,补充完成下面的统计分析表.
| 运动员 | 平均数 | 众数 | 中位数 | 方差 |
| 甲 | 601.8 | 600 | 600 | 50.56 |
| 乙 | 599.3 | 618 | 595.5 | 284.21 |
20.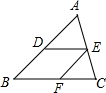 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B. | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C. | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D. | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
10.下面的数中,比0小的是( )
| A. | $\frac{1}{2}$ | B. | 0.01 | C. | |-l| | D. | -2013 |
5.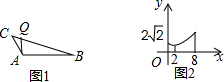 如图1,在钝角△ABC中,点Q从点C开始出发向点B运动,在运动过程中,设线段CQ的长为x,线段AQ的长为y,y关于x的函数图象如图2所示,横坐标为2时,是函数图象的最低点,则下列说法不正确的是( )
如图1,在钝角△ABC中,点Q从点C开始出发向点B运动,在运动过程中,设线段CQ的长为x,线段AQ的长为y,y关于x的函数图象如图2所示,横坐标为2时,是函数图象的最低点,则下列说法不正确的是( )
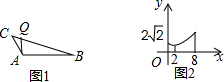 如图1,在钝角△ABC中,点Q从点C开始出发向点B运动,在运动过程中,设线段CQ的长为x,线段AQ的长为y,y关于x的函数图象如图2所示,横坐标为2时,是函数图象的最低点,则下列说法不正确的是( )
如图1,在钝角△ABC中,点Q从点C开始出发向点B运动,在运动过程中,设线段CQ的长为x,线段AQ的长为y,y关于x的函数图象如图2所示,横坐标为2时,是函数图象的最低点,则下列说法不正确的是( )| A. | ∠C的度数为45° | B. | AQ的最小值为2 | C. | △ABC的面积为8 | D. | sinB的值为$\frac{1}{3}$ |
6.下列图形:①等腰三角形;②平行四边形;③矩形;④菱形;⑤正方形.用两个全等但不是等腰的直角三角形,一定能拼成的是( )
| A. | ①②③ | B. | ②③④ | C. | ①③⑤ | D. | ①②③④⑤ |