题目内容
9.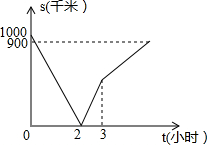 甲、乙、丙三地在一条直线上,乙地在甲地和丙地之间,一列高速列车从甲地开往乙地,一列快速列车从丙地经乙地开往甲地,两列列车同时出发,匀速行驶,且到达各自目的地后停止运行,从两列列车出发开始,至快速列车到达甲地为止,两列列车的距离s(千米)与行驶时间t(小时)之间的函数图象如图所示
甲、乙、丙三地在一条直线上,乙地在甲地和丙地之间,一列高速列车从甲地开往乙地,一列快速列车从丙地经乙地开往甲地,两列列车同时出发,匀速行驶,且到达各自目的地后停止运行,从两列列车出发开始,至快速列车到达甲地为止,两列列车的距离s(千米)与行驶时间t(小时)之间的函数图象如图所示(1)甲、丙两地之间的距离是1000千米;
(2)求两列列车的速度;
(3)请直接写出s与t之间的函数关系式,并写出自变量t的取值范围.
分析 (1)当t=0时,s=1000,由此可知甲、丙两地之间的距离;
(2)设高速列车的速度为x千米/时,快速列车的速度为y千米/时,根据路程=速度×时间,可列出关于x、y的二元一次方程组,解方程组即可得出结论;
(3)结合(2)中的速度,根据时间=路程÷速度可寻找出图象各拐点的坐标,设s关于t的函数关系式为y=kt+b,分段利用待定系数法即可寻找函数关系式.
解答 解:(1)当t=0时,s=1000,
∴甲、丙两地之间的距离是1000千米.
故答案为:1000.
(2)设高速列车的速度为x千米/时,快速列车的速度为y千米/时,
由题意知:$\left\{\begin{array}{l}{2(x+y)=1000}\\{3x=900}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=300}\\{y=200}\end{array}\right.$.
答:高速列车的速度为300千米/时,快速列车的速度为200千米/时.
(3)设s关于t的函数关系式为y=kt+b,
①当0≤t<2时,有$\left\{\begin{array}{l}{b=1000}\\{2k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-500}\\{b=1000}\end{array}\right.$.
此时s=-500t+1000;
②当t=3时,两车之间的距离为(300+200)×(3-2)=500(千米),
当2≤t<3时,有$\left\{\begin{array}{l}{2k+b=0}\\{3k+b=500}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=500}\\{b=-1000}\end{array}\right.$.
此时s=500t-1000;
③快速列车到达甲地的时间为1000÷200=5(小时),
当3≤t≤5时,有$\left\{\begin{array}{l}{3k+b=500}\\{5k+b=900}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=200}\\{b=-100}\end{array}\right.$.
此时s=200t-100.
综上可知:s与t之间的函数关系式为s=$\left\{\begin{array}{l}{-500t+1000(0≤t<2)}\\{500t-1000(2≤t<3)}\\{200t-100(3≤t≤5)}\end{array}\right.$.
点评 本题考查了一次函数的应用、二元一次方程组的应用以及待定系数法求函数关系式,解题的关键是:(1)令t=0找出s=1000;(2)利用数量关系列出关于x、y的二元一次方程组;(3)找出各拐点的坐标利用待定系数法求函数关系式.本题属于中档题,(1)没有难度;(2)需结合图形分析出何时高铁到达乙地;(3)由数量关系寻找各拐点坐标,深刻体现了数形结合的好处.

 考前必练系列答案
考前必练系列答案| A. | a2+a2=a4 | B. | (-a2)3=(-a)6 | C. | [(-a)2]3=a6 | D. | (a2)3÷a2=a3 |
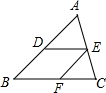 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B. | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C. | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D. | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
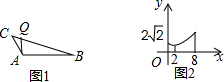 如图1,在钝角△ABC中,点Q从点C开始出发向点B运动,在运动过程中,设线段CQ的长为x,线段AQ的长为y,y关于x的函数图象如图2所示,横坐标为2时,是函数图象的最低点,则下列说法不正确的是( )
如图1,在钝角△ABC中,点Q从点C开始出发向点B运动,在运动过程中,设线段CQ的长为x,线段AQ的长为y,y关于x的函数图象如图2所示,横坐标为2时,是函数图象的最低点,则下列说法不正确的是( )| A. | ∠C的度数为45° | B. | AQ的最小值为2 | C. | △ABC的面积为8 | D. | sinB的值为$\frac{1}{3}$ |
| A. | ②④ | B. | ①③ | C. | ①③④ | D. | ①②③④ |
 如图,已知AB∥DE,CD∥BF,则∠B与∠D的度数和为( )
如图,已知AB∥DE,CD∥BF,则∠B与∠D的度数和为( )| A. | 90° | B. | 150° | C. | 180° | D. | 无法确定 |
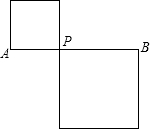 如图,AB=n,P是线段AB上一点,分别以AP、BP为边作正方形.
如图,AB=n,P是线段AB上一点,分别以AP、BP为边作正方形.