题目内容
14．（1）计算：$\sqrt{9}$+（-$\frac{1}{2}$）-1-$\sqrt{2}$sin45°+（$\sqrt{3}$-2）0（2）解方程：$\frac{3}{x-1}=\frac{2}{x+1}$．
分析 （1）原式第一项利用算术平方根定义计算，第二项利用负整数指数幂法则计算，第三项利用特殊角的三角函数值计算，最后一项利用零指数幂法则计算即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）原式=3-2-$\sqrt{2}$×$\frac{\sqrt{2}}{2}$+1=3-2-1+1=1；
（2）去分母得：3x+3=2x-2，
解得：x=-5，
经检验x=-5是分式方程的解．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
13．某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛，在最近的10次选拔赛中，这两个人的跳远成绩（单位：cm）如图所示，请根据图中信息，解答下列问题：
（1）通过计算，补充完成下面的统计分析表．
（2）请依据对上述统计信息的数据分析，说明这两名运动员的成绩各有什么特点？
（1）通过计算，补充完成下面的统计分析表．
| 运动员 | 平均数 | 众数 | 中位数 | 方差 |
| 甲 | 601.8 | 600 | 600 | 50.56 |
| 乙 | 599.3 | 618 | 595.5 | 284.21 |
5．
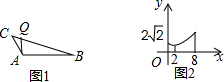如图1，在钝角△ABC中，点Q从点C开始出发向点B运动，在运动过程中，设线段CQ的长为x，线段AQ的长为y，y关于x的函数图象如图2所示，横坐标为2时，是函数图象的最低点，则下列说法不正确的是（ ）
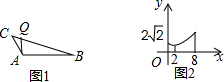如图1，在钝角△ABC中，点Q从点C开始出发向点B运动，在运动过程中，设线段CQ的长为x，线段AQ的长为y，y关于x的函数图象如图2所示，横坐标为2时，是函数图象的最低点，则下列说法不正确的是（ ）| A． | ∠C的度数为45° | B． | AQ的最小值为2 | C． | △ABC的面积为8 | D． | sinB的值为$\frac{1}{3}$ |
如图，直线AB、CD交于点O，∠AOC：∠BOC=4：5，且OE⊥CD，则∠AOE=10度．
9．
如图，已知AB∥DE，CD∥BF，则∠B与∠D的度数和为（ ）
如图，已知AB∥DE，CD∥BF，则∠B与∠D的度数和为（ ）| A． | 90° | B． | 150° | C． | 180° | D． | 无法确定 |
6．下列图形：①等腰三角形；②平行四边形；③矩形；④菱形；⑤正方形．用两个全等但不是等腰的直角三角形，一定能拼成的是（ ）
| A． | ①②③ | B． | ②③④ | C． | ①③⑤ | D． | ①②③④⑤ |