题目内容
12. 如图,观察每一个图中黑色正六边形的排列规律,第10个图中黑色正六边形有100个,第n个图中黑色正六边形有n2个.
如图,观察每一个图中黑色正六边形的排列规律,第10个图中黑色正六边形有100个,第n个图中黑色正六边形有n2个.
分析 从图案分析可知,第1个图中黑色正六边形的个数都是1的平方,第2个图中黑色正六边形的个数都是2的平方,第3个图中黑色正六边形的个数都是3的平方,依此类推可得规律:第n个图中黑色正六边形有n2个,那么第10个图中黑色正六边形个数可求.
解答 解:第1个图中黑色正六边形的个数是:12=1,
第2个图中黑色正六边形的个数是:22=4,
第3个图中黑色正六边形的个数是:32=9,
…
第n个图中黑色正六边形有n2个.
第10个图中黑色正六边形的个数是:102=100.
故答案为:100,n2.
点评 本题主要考查图形的变化规律,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
相关题目
7.用“O”摆出如图所示的图案,若按照同样的方式构造图案,则第10个图案需要“O”的个数是( )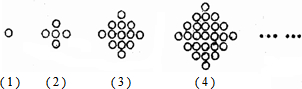

| A. | 145个 | B. | 162 | C. | 181个 | D. | 202个 |
2.某班主任老师为了对学生乱花钱的现象进行教育指导,对班里每位同学一周大约花钱数额进行了统计,如下表:
根据这个统计可知,该班学生一周花钱数额的众数、中位数是( )
| 花钱数额(元) | 5 | 10 | 15 | 20 | 25 |
| 学生人数 | 7 | 12 | 18 | 10 | 3 |
| A. | 15,15 | B. | 18,15 | C. | 25,18 | D. | 15,18 |
 如图,等腰直角△ABC中,∠ACB=90°,点D在BA的延长线上,连接CD,过点C作CE⊥CD,使CE=CD,连接BE,若点N为BD的中点,连接CN、BE.
如图,等腰直角△ABC中,∠ACB=90°,点D在BA的延长线上,连接CD,过点C作CE⊥CD,使CE=CD,连接BE,若点N为BD的中点,连接CN、BE.
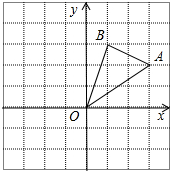 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O顺时针旋转90°后得到△A1OB1.