Question

4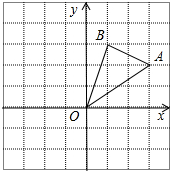．如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O顺时针旋转90°后得到△A₁OB₁．
①点A关于点O中心对称的点的坐标为（-3，-2）；
②写出经过点A₁的反比例函数解析式为y=-$\frac{6}{x}$；
③在旋转过程中，点B经过的路径为弧BB₁，求弧BB₁的长．

Answer 1

分析 （1）根据关于原点对称的点的坐标特征求解；
（2）根据画法得到点A₁的坐标为（2，-3），然后利用待定系数法求反比例函数解析式；
（3）先利用勾股定理计算OB，然后根据弧长公式求解．

解答 解：（1）点A（3，2）关于点O中心对称的点的坐标为（-3，-2）；
（2）如图，

设经过为点A₁的反比例函数解析式为y=$\frac{k}{x}$，
由图形可得点A₁的坐标为（2，-3），
所以k=2×（-3）=-6，
所以经过点A₁的反比例函数解析式为y=-$\frac{6}{x}$；
（3）OB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
所以弧BB₁的长=$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{10}}{2}$π．
故答案为（-3，-2），y=-$\frac{6}{x}$．

点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了待定系数法求反比例函数解析式和弧长的计算．