题目内容
17.古希腊著名的毕达哥拉斯学派把1、3、6、10 …这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.请根据这一规律写出第6个图形表示的等式49=21+28.
分析 观察图象中点的个数的规律有第一个图形是4=22=1+2+1,第二个图形是9=32=1+2+3+2+1,第三个图形是16=42=1+2+3+4+3+2+1,…则按照此规律得到第6个图形的规律即可.
解答 解:∵第1个图形是4=22=1+2+1,
第2个图形是9=32=1+2+3+2+1,
第3个图形是16=42=1+2+3+4+3+2+1,
…
∴第6个图形是72=1+2+3+4+5+6+7+6+5+4+3+3+2+1=28+21.
故答案为:49=21+28.
点评 此题考查图形的变化规律,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
2.关于相反数的意义,下列说法正确的是( )
| A. | 一正一负的两个有理数(零除外)称之为相反数 | |
| B. | 具有相反意义的两个数称之为相反数 | |
| C. | 在数轴上原点的两旁,离开原点距离相等的点所表示的两个数 | |
| D. | 符号不同的两个数 |
8.春节前夕,某商店购进了一批衣服,每件衣服的进价为a元,将其价格提高40%后,再以九折出售,则这件衣服的售价是( )
| A. | 0.9a元 | B. | 1.2a元 | C. | 1.26a元 | D. | 1.4a元 |
6.钩鱼岛是我国的固有领土,这段时间,中日钩鱼岛事件成了各大新闻网站的热点话题.小芳在“百度”搜索引擎中输入“钩鱼岛事件最新进展”,能搜索到相关结果约20300000个,20300000这个数用科学记数法表示为( )
| A. | 2.03×106 | B. | 20.3×106 | C. | 2.03×107 | D. | 0.203×108 |
7.数据8,6,7,9,3,9,5的众数与中位数分别是( )
| A. | 6,7 | B. | 9,5 | C. | 9,7 | D. | 3,5 |
 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“镇”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“镇”相对的面上的汉字是( ) 如图,观察每一个图中黑色正六边形的排列规律,第10个图中黑色正六边形有100个,第n个图中黑色正六边形有n2个.
如图,观察每一个图中黑色正六边形的排列规律,第10个图中黑色正六边形有100个,第n个图中黑色正六边形有n2个.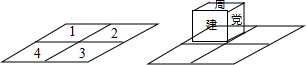 如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号.
如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号. 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,并分别找出它们的中点M,N.若测得MN=15m,则A,B两点间的距离为( )m.
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,并分别找出它们的中点M,N.若测得MN=15m,则A,B两点间的距离为( )m.