题目内容
7.已知△ABC的三边长为AB=2,BC=3,AC=4,则三角形内切圆半径为( )| A. | $\frac{\sqrt{15}}{2}$ | B. | $\frac{\sqrt{15}}{6}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{15}}{4}$ |
分析 作AD⊥BC于D,根据直角三角形的性质和勾股定理求出AD、DC的长,根据三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r计算即可.
解答 解:过点C作CD⊥AB,垂足为D,
设AD=x,则BD=2-x,
由勾股定理得:CD2=AC2-AD2,CD2=BC2-BD2.
∴42-x2=32-(2-x)2.
解得:x=2.75.
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{4}^{2}-2.7{5}^{2}}$=$\frac{3\sqrt{15}}{4}$,
由△ABC的面积=$\frac{1}{2}$×(AB+BC+AC)×r可知:$\frac{1}{2}×2×\frac{3\sqrt{15}}{4}$=$\frac{1}{2}×$(2+3+4)×(8+5+7)r,
解得:r=$\frac{\sqrt{15}}{6}$,
故选B.
点评 本题主要考查的是勾股定理的定义、三角形的内心,明确三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
17.下列不等式组无解的是( )
| A. | $\left\{\begin{array}{l}{x+1<0}\\{x-2>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-1<0}\\{x+2>0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+1>0}\\{x-2>0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-2<0}\\{x+1<0}\end{array}\right.$ |
2.已知x=m是方程x2-x-2016=0的一个解,则代数式m2-$\frac{2016}{m}$的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
17.下列运算正确的是( )
| A. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | B. | $\sqrt{2}$+1=$\sqrt{3}$ | C. | $\sqrt{7}$-$\sqrt{5}$=$\sqrt{2}$ | D. | 6$\sqrt{2}$+$\sqrt{2}$=7$\sqrt{2}$ |
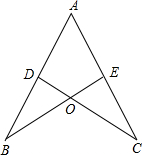 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.