题目内容
12.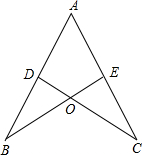 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.(1)求证:AD=AE;
(2)若AB=10,AE=6,求BO的长.
分析 (1)欲证明AD=AE,只要证明△ADC≌△AEB即可.
(2)先利用勾股定理求出BE,再证明△BDO∽△BEA,得$\frac{BD}{BE}$=$\frac{BO}{AB}$,由此即可解决问题.
解答 (1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
在△ADC和△AEB中,
$\left\{\begin{array}{l}{∠A=∠A}\\{∠ADC=∠AEB}\\{AC=AB}\end{array}\right.$,
∴△ADC≌△AEB,
∴AD=AE.
(2)解:∵AD=AE,AE=6,AB=10,
∴BD=10-6=4,
在RT△ABE中,BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵∠B=∠B,∠BDO=∠AEB=90°,
∴△BDO∽△BEA,
∴$\frac{BD}{BE}$=$\frac{BO}{AB}$,
∴$\frac{4}{8}$=$\frac{BO}{10}$,
∴BO=5.
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是熟练掌握全等三角形和相似三角形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目
2.古希腊数学家把数1,3,6,10,15,21,…叫做三角数,它有一定的规律性.若把第一个三角数记为a1,第二个三角数记为a2,…,第n个三角数记为an,则an-1+an=( )( )
| A. | (n-1)2 | B. | n2 | C. | (n+1)2 | D. | (n+2)2 |
7.已知△ABC的三边长为AB=2,BC=3,AC=4,则三角形内切圆半径为( )
| A. | $\frac{\sqrt{15}}{2}$ | B. | $\frac{\sqrt{15}}{6}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{15}}{4}$ |
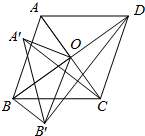 已知:菱形ABCD的对角线AC,BD相交于点O,将△AOB绕点O逆时针方向旋转得到△A′OB′,旋转角为α(0°<α<90°),连接A′C,B′D,B′B,且AC=6,AD=5.
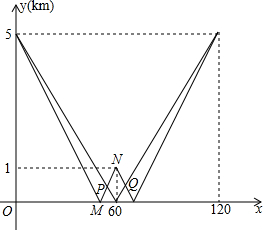
已知:菱形ABCD的对角线AC,BD相交于点O,将△AOB绕点O逆时针方向旋转得到△A′OB′,旋转角为α(0°<α<90°),连接A′C,B′D,B′B,且AC=6,AD=5.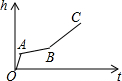 匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则对应的这个容器的形状为( )
匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则对应的这个容器的形状为( )
 在一次徒步活动中,有甲、乙两支徒步队伍.队伍甲由A地步行到B地后按原路返回,队伍乙由A地步行经B地继续前行到C地后按原路返回,甲、乙两支队伍同时出发.设步行时间为x(分钟),甲、乙两支队伍距B地的距离为y1(千米)和y2(千米).(甲、乙两队始终保持匀速运动)图中的折线分别表示y1、y2与x之间的函数关系,请你结合所给的信息回答下列问题:
在一次徒步活动中,有甲、乙两支徒步队伍.队伍甲由A地步行到B地后按原路返回,队伍乙由A地步行经B地继续前行到C地后按原路返回,甲、乙两支队伍同时出发.设步行时间为x(分钟),甲、乙两支队伍距B地的距离为y1(千米)和y2(千米).(甲、乙两队始终保持匀速运动)图中的折线分别表示y1、y2与x之间的函数关系,请你结合所给的信息回答下列问题: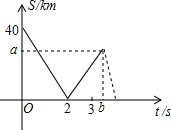 A、B两地之间路程是350km,甲、乙两车从A地以各自的速度匀速行驶到B地,甲车先出发半小时,乙车到达B地后原地休息等待甲车到达.如图是甲、乙两车之间的路程S(km)与乙车出发时间t(h)之间的函数关系的图象.
A、B两地之间路程是350km,甲、乙两车从A地以各自的速度匀速行驶到B地,甲车先出发半小时,乙车到达B地后原地休息等待甲车到达.如图是甲、乙两车之间的路程S(km)与乙车出发时间t(h)之间的函数关系的图象.