题目内容
15.阅读材料:已知m=$\frac{1}{2-\sqrt{3}}$,求2m2-8m+3的值.解:∵m=$\frac{1}{2-\sqrt{3}}$=$\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}$=2+$\sqrt{3}$.
∴m-2=$\sqrt{3}$,∴(m-2)2=3,m2-4m+4=3
∴m2-4m=-1,
∴2m2-8m+3=2(m2-4m)+3=2×(-1)+3=1
请根据以上的分析过程,解决下列问题:
(1)化简$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{2+\sqrt{3}}$+…+$\frac{1}{3+2\sqrt{2}}$;
(2)若n=$\frac{1}{\sqrt{2}-1}$,
①求4n2-8n+1的值;
②请直接写出以下代数式的值:
4n3-9n2-2n+1=0;
3n2-7n+$\frac{1}{n}$+4=5.
分析 (1)首先找出有理化因式进而化简求出答案;
(2)①首先化简n的值,进而将原式变形求出答案;
②将原式变形进而将已知代入求出答案.
解答 解:(1)$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{2+\sqrt{3}}$+…+$\frac{1}{3+2\sqrt{2}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$+…+3-2$\sqrt{2}$
=2;
(2)∵n=$\frac{1}{\sqrt{2}-1}$,
∴n=$\sqrt{2}$+1,
则n-1=$\sqrt{2}$,
①4n2-8n+1=4(n-1)2-3=4×2-3=5;
②4n3-9n2-2n+1
=n(4n2-8n)-n2-2n+1
=4n-n2-2n+1
=-(n2-2n)+1
=-(n-1)2+2
=-($\sqrt{2}$+1-1)2+2
=0;
3n2-7n+$\frac{1}{n}$+4
=3($\sqrt{2}$+1)2-7($\sqrt{2}$+1)+$\sqrt{2}$-1+4
=3(3+2$\sqrt{2}$)-7$\sqrt{2}$-7+$\sqrt{2}$+3
=5.
故答案为:0,5.
点评 此题主要考查了分母有理化,正确得出有理化因式是解题关键.

练习册系列答案
相关题目
10.下列运算中,正确的是( )
| A. | 2xa+xa=3x2a2 | B. | (a2)3=a6 | C. | 3a•2a=6a | D. | 3-2=-6 |
7.已知△ABC的三边长为AB=2,BC=3,AC=4,则三角形内切圆半径为( )
| A. | $\frac{\sqrt{15}}{2}$ | B. | $\frac{\sqrt{15}}{6}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{15}}{4}$ |
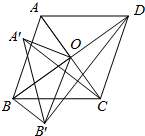 已知:菱形ABCD的对角线AC,BD相交于点O,将△AOB绕点O逆时针方向旋转得到△A′OB′,旋转角为α(0°<α<90°),连接A′C,B′D,B′B,且AC=6,AD=5.
已知:菱形ABCD的对角线AC,BD相交于点O,将△AOB绕点O逆时针方向旋转得到△A′OB′,旋转角为α(0°<α<90°),连接A′C,B′D,B′B,且AC=6,AD=5.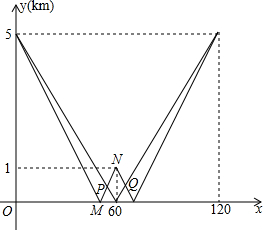 在一次徒步活动中,有甲、乙两支徒步队伍.队伍甲由A地步行到B地后按原路返回,队伍乙由A地步行经B地继续前行到C地后按原路返回,甲、乙两支队伍同时出发.设步行时间为x(分钟),甲、乙两支队伍距B地的距离为y1(千米)和y2(千米).(甲、乙两队始终保持匀速运动)图中的折线分别表示y1、y2与x之间的函数关系,请你结合所给的信息回答下列问题:
在一次徒步活动中,有甲、乙两支徒步队伍.队伍甲由A地步行到B地后按原路返回,队伍乙由A地步行经B地继续前行到C地后按原路返回,甲、乙两支队伍同时出发.设步行时间为x(分钟),甲、乙两支队伍距B地的距离为y1(千米)和y2(千米).(甲、乙两队始终保持匀速运动)图中的折线分别表示y1、y2与x之间的函数关系,请你结合所给的信息回答下列问题: