题目内容
3. 已知抛物线y=-$\frac{1}{2}$x2+4x-6.
已知抛物线y=-$\frac{1}{2}$x2+4x-6.(1)求抛物线与x轴、y轴的交点坐标及顶点坐标;
(2)画出所给函数的图象.
分析 (1)令x=0,则能够求出y轴交点的坐标,令y=0,则能够求出和x轴交点的坐标,再用配方法求出其顶点的坐标,进而求出y轴交点、与x轴交点、及顶点的坐标;
(2)根据函数与y轴交点、与x轴交点、及顶点的坐标画出图象即可.
解答 解:(1)令x=0,则y=-6,所以抛物线和y轴的交点A(0,-6),
令y=0,则y=-$\frac{1}{2}$x2+4x-6=0,解得:x=6或2,所以抛物线和x轴交点的坐标为B(2,0),C(6,0);
因为y=-$\frac{1}{2}$x2+4x-6=-$\frac{1}{2}$(x-4)2+2,
所以顶点的坐标为D(4,2);
(2)函数图象如图,
点评 本题考查了求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与坐标轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标,和y轴的交点是令x=0.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
8.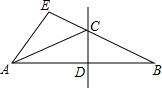 如图,△ABE中,CD是线段AB的垂直平分线,如果AE=4cm,△ACE的周长为11cm,则BE长为( )
如图,△ABE中,CD是线段AB的垂直平分线,如果AE=4cm,△ACE的周长为11cm,则BE长为( )
 如图,△ABE中,CD是线段AB的垂直平分线,如果AE=4cm,△ACE的周长为11cm,则BE长为( )
如图,△ABE中,CD是线段AB的垂直平分线,如果AE=4cm,△ACE的周长为11cm,则BE长为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
 如图,是一个正方体表面展开图,请在图中空格内填上适当的数,使这个正方体相对两个面上标注的数值相等(将答案填在图中空格内)
如图,是一个正方体表面展开图,请在图中空格内填上适当的数,使这个正方体相对两个面上标注的数值相等(将答案填在图中空格内)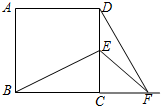 已知,如图正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.
已知,如图正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.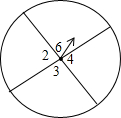 把带有指针的圆形转盘分成4等分,并且在每一区域内标上数字,小红、小明两个人玩转盘游戏,规则是:转动转盘,当转盘停止时,指针指向区域的数字是偶数,则小红胜;若指针指向区域的数字为奇数,则小明胜;若指针落在分割线上,则无效,需重新转动转盘.分别求出小红、小明获胜的概率.
把带有指针的圆形转盘分成4等分,并且在每一区域内标上数字,小红、小明两个人玩转盘游戏,规则是:转动转盘,当转盘停止时,指针指向区域的数字是偶数,则小红胜;若指针指向区域的数字为奇数,则小明胜;若指针落在分割线上,则无效,需重新转动转盘.分别求出小红、小明获胜的概率.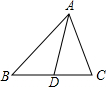 如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是1<AD<4.
如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是1<AD<4.