题目内容
12.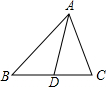 如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是1<AD<4.
如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是1<AD<4.
分析 延长AD至E,使DE=AD,连接CE.根据SAS证明△ADC≌△EDB,得BE=AC,再根据三角形的三边关系即可求解.
解答  解:延长AD至E,使DE=AD,连接CE.
解:延长AD至E,使DE=AD,连接CE.
在△ADC和△EDB中,
$\left\{\begin{array}{l}{AD=ED}\\{∠ADC=∠EDB}\\{BD=CD}\end{array}\right.$,
∴△ADC≌△EDB,
∴BE=AC=3.
在△ABE中,AB-BE<AE<AB+BE,
即2<2AD<8,
1<AD<4.
故答案为1<AD<4.
点评 此题考查了全等三角形的判定和性质、三角形的三边关系.正确作出辅助线,把求AD的长的范围的问题转化为三角形的三边关系问题是关键.

练习册系列答案
相关题目
2.下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图形中白色正方形的个数为( )


| A. | 20 | B. | 30 | C. | 32 | D. | 34 |
17.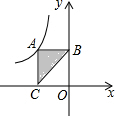 如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
 如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )| A. | 12 | B. | 6 | C. | 3 | D. | $\frac{3}{2}$ |
 已知抛物线y=-$\frac{1}{2}$x2+4x-6.
已知抛物线y=-$\frac{1}{2}$x2+4x-6. 如图,方格纸中△ABC的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,则在图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是4个.
如图,方格纸中△ABC的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,则在图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是4个.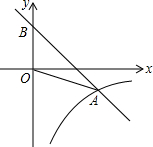 如图,平面直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上一点,一次函数y2=-x+2的图象经过点A,交y轴于点B,△AOB的面积是3.
如图,平面直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上一点,一次函数y2=-x+2的图象经过点A,交y轴于点B,△AOB的面积是3. 如图,若使△ACD∽△ABC,需添加的一个条件是∠ACD=∠B.
如图,若使△ACD∽△ABC,需添加的一个条件是∠ACD=∠B.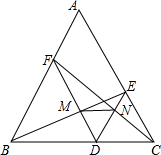 如图,在正△ABC中,DE∥AB,DF∥AC,求证:△MDN是等边三角形.
如图,在正△ABC中,DE∥AB,DF∥AC,求证:△MDN是等边三角形.