题目内容
13.已知关于x的方程kx2-(3k-1)x+2(k-1)=0,求证:无论k为何实数,方程总有实数根.分析 分两种情况讨论:①当k=0时,方程是一元一次方程,有实数根;②当k≠0时,方程是一元二次方程,所以证明判别式是非负数即可;
解答 证明:①当k=0时,x-2=0,得x=2,有实数根;
②当k≠0时,方程是一元二次方程,
∵△=(3k-1)2-4k×2(k-1)=(k+1)2≥0,
∴无论k为何实数,方程总有实数根;
综上所述,无论k为何实数,方程总有实数根.
点评 本题主要考查一元二次方程根的判别式和根与系数的关系的应用,同时考查了学生的综合应用能力及推理能力.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8.下列计算正确的是( )
| A. | (-2)-(-5)=-7 | B. | (+3)+(-6)=3 | C. | (+5)-(-8)=-3 | D. | (-5)-(-8)=3 |
 已知抛物线y=-$\frac{1}{2}$x2+4x-6.
已知抛物线y=-$\frac{1}{2}$x2+4x-6.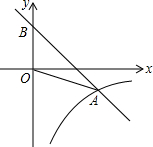 如图,平面直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上一点,一次函数y2=-x+2的图象经过点A,交y轴于点B,△AOB的面积是3.
如图,平面直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上一点,一次函数y2=-x+2的图象经过点A,交y轴于点B,△AOB的面积是3. 如图,若使△ACD∽△ABC,需添加的一个条件是∠ACD=∠B.
如图,若使△ACD∽△ABC,需添加的一个条件是∠ACD=∠B.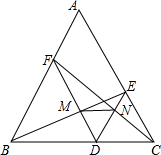 如图,在正△ABC中,DE∥AB,DF∥AC,求证:△MDN是等边三角形.
如图,在正△ABC中,DE∥AB,DF∥AC,求证:△MDN是等边三角形. 如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.
如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.