题目内容
6.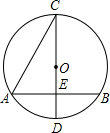 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )| A. | 30° | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | 2 |
分析 如图,作辅助线;运用射影定理分别求出DE、CE、AC的长度,借助正弦函数的定义即可解决问题.
解答  解:如图,连接AD;
解:如图,连接AD;
∵CD为⊙O的直径,且CD⊥AB,
∴∠DAC=90°,AE=BE=4;
设DE=λ,则CE=10-λ,
由射影定理得:42=λ(10-λ),
解得:λ=2或8(设去),
∴CE=10-2=8,
由射影定理得:AC2=CE•CD,
解得:AC=4$\sqrt{5}$,
∴sin∠ACD=$\frac{AE}{AC}$=$\frac{\sqrt{5}}{5}$,
故选C.
点评 该题主要考查了垂径定理、射影定理等几何知识点及其应用问题;解题的关键是作辅助线,构造直角三角形,灵活运用垂径定理、射影定理等几何知识点来分析、判断、解答.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
11.如果不等式组$\left\{\begin{array}{l}{x+2a≥4}\\{\frac{2x-b}{3}<1}\end{array}\right.$的解集是0≤x<1,那么a+b的值为1.
18.已知n是一个正整数,若$\sqrt{135n}$与$\sqrt{3}$能合并,则n的最小值是( )
| A. | 3 | B. | 5 | C. | 15 | D. | 25 |
13.若ab=cd,且abcd≠0,则下列式子正确的是( )
| A. | a:c=b:d | B. | d:c=b:a | C. | a:b=c:d | D. | a:d=c:b |