题目内容
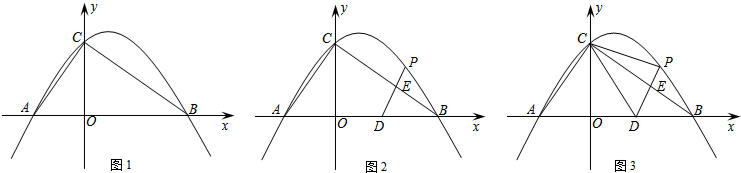
16.在抛物线y=x2+(a-1)x+1,在1≤x≤3时,x=1有最大值,求a的取值范围.分析 由于二次函数的顶点坐标不能确定,故应分对称轴不在[1,3]和对称轴在[1,3]内两种情况进行解答.
解答 解:第一种情况:
当二次函数的对称轴不在1≤x≤3内时,此时,对称轴一定在1≤x≤3的右边,函数方能在这个区域取得最大值,
x=$\frac{1-a}{2}$>3,即a<-5,
第二种情况:
当对称轴在1≤x≤3内时,对称轴一定是在区间1≤x≤3的中点的右边,因为如果在中点的左边的话,就是在x=3的地方取得最大值,即:
x=$\frac{1-a}{2}$≥$\frac{1+3}{2}$,即a≤-3(此处若a取-3的话,函数就在1和3的地方都取得最大值)
综合上所述a≤-3.
点评 本题考查了二次函数的最值确定与自变量x的取值范围的关系,难度较大.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
6.下列式子不是二次根式的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{a}$(a≥0) | C. | $\sqrt{{a^2}+1}$ | D. | $\sqrt{-2}$ |
11.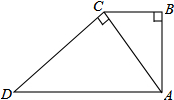 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )| A. | 2:3 | B. | 3:5 | C. | 9:25 | D. | $\sqrt{3}$:$\sqrt{5}$ |
6.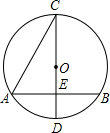 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )| A. | 30° | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | 2 |