题目内容
11.如果不等式组$\left\{\begin{array}{l}{x+2a≥4}\\{\frac{2x-b}{3}<1}\end{array}\right.$的解集是0≤x<1,那么a+b的值为1.分析 先分别解两个不等式得到x≥4-2a和x<$\frac{3+b}{2}$,再利用不等式组的解集是0≤x<1得到4-2a=0,$\frac{3+b}{2}$=1,解方程求出a和b的值,然后计算a+b.
解答 解:$\left\{\begin{array}{l}{x+2a≥4①}\\{\frac{2x-b}{3}<1②}\end{array}\right.$,
解①得x≥4-2a,
解②得x<$\frac{3+b}{2}$,
而不等式组的解集是0≤x<1,
所以4-2a=0,$\frac{3+b}{2}$=1,解得a=2,b=-1,
所以a+b=2-1=1.
故答案为1.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
6.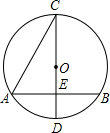 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )| A. | 30° | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | 2 |
18.下列数据不能确定物体的位置的是( )
| A. | 南偏西40° | B. | 某电影院5排21号 | ||
| C. | 大桥南路38号 | D. | 北纬21°,东经115° |
 如图,在?ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F,已知?ABCD的周长是14,OF=1.3,求四边形BCFE的周长.
如图,在?ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F,已知?ABCD的周长是14,OF=1.3,求四边形BCFE的周长.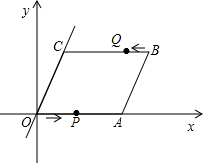 如图,在直角坐标系中,点O是坐标原点,四边形OABC是平行四边形,点A的坐标为(14,0),点B的坐标为(18,4$\sqrt{3}$)
如图,在直角坐标系中,点O是坐标原点,四边形OABC是平行四边形,点A的坐标为(14,0),点B的坐标为(18,4$\sqrt{3}$)