题目内容

15．已知a＞b＞c，M=a2b+b2c+c2a，N=ab2+bc2+ca2，试判断M与N的大小关系．

分析 多项式比较大小，采用“作差法”，将多项式因式分解，再根据已知条件判断M-N的符号．

解答 解：∵M-N=（a2b+b2c+c2a）-（ab2+bc2+ca2），
=a2b+b2c+c2a-ab2-bc2-ca2，
=a2（b-c）+b2（c-a）+c2（a-b），
=a2（b-c）+bc（b-c）-ab2+ac2，
=a2（b-c）+bc（b-c）-a（b+c）（b-c），
=（b-c）（a2+bc-ab-ac），
=（b-c）（a-c）（a-b），
又a＞b＞c，
∴M-N=（b-c）（a-c）（a-b）＞0，
即M＞N．

点评 本题考查了因式分解的实际运用，用作差法比较整式的大小是常用的方法：当M-N＞0时，M＞N，当M-N=0时，M=N，当M-N＜0时，M＜N．

练习册系列答案
相关题目
5．计算：$\sqrt{6{x}^{2}}$÷$\sqrt{12{x}^{3}y}$（y＞0）．
6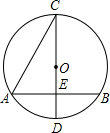．如图，AB，CD分别是⊙O的弦和直径，AB⊥CD于点E，若CD=10，AB=8，则sin∠ACD的值为（　　）
A．30°B．$\frac{1}{2}$C．$\frac{\sqrt{5}}{5}$D．2
3．数据：6，5，4，2，8的平均数是5．
10．一棵挺直的松树高18米，一阵强风将其折断，树尖B落在离树的底端O点12米处，求该树断处的高度OA．
20．计算：
（1）$\frac{2x-y}{x}-\frac{y}{y-2x}$；
（2）（-12x2y）2÷（-$\frac{3{x}^{2}}{y}$）2
（3）$\frac{2x-4}{{x}^{2}+3}÷\frac{x-2}{{x}^{2}+6x+9}$．
4．阅读材料：
对于任意两个数a、b的大小比较，有下面的方法：
当a-b＞0时，一定有a＞b；
当a-b=0时，一定有a=b；
当a-b＜0时，一定有a＜b．
反过来也成立．因此，我们把这种比较两个数大小的方法叫做“求差法”．
问题解决：
（1）图1长方形的周长M=2a+4b+2c；图2长方形的周长N=2a+2b+4c；用“求差法”比较M、N的大小（b＞c）．
（2）如图3，把边长为a+b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个长方形，试比较两个小正方形面积之和A与两个长方形面积之和B的大小．
1．【已知】在Rt△ABC中，∠C=90°，BC=3，AC=4，P为AC边上的一动点．
操作：请在图1中以PA，PB为边作?APBQ（保留作图痕迹，不写作法），并连接PQ交AB于点M．
【探究】（1）在点P运动过程中，对角线PQ的最小值为3，此时$\frac{AP}{AC}$的值为$\frac{1}{2}$；
【温馨提示】若你在探究此问题时出现困难，可参考如下分析思路：端点分别在两条平行线上的所有线段中，垂直于平行线的线段最短．
（2）如图2，若延长PA到点E，使AE=nPA（n为大于0的常数），以PE、PB为边作?PBQE，求对角线PQ的最小值和此时$\frac{AP}{AC}$的值；
【拓展】如图3，若P为AB边上的一动点，延长PA到点E，使AE=nPA（n为大于0的常数），以PE、PC为边作?PCQE．则对角线PQ的最小值为$\frac{12}{5}$，此时$\frac{AP}{AC}$的值为$\frac{4}{5（n+2）}$．
2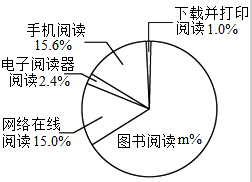．根据某研究院公布的2010-2014年我国成年国民阅读调查报告的部分相关数据，绘制的统计图表如下：
年份年人均阅读图书数量（本）
20103.8
20114.1
20124.3
20134.6
20144.8
根据以上信息解答下列问题：
（1）直接写出扇形统计图中m的值；
（2）从2010到2014年，成年居民年人均阅读图书的数量每年增长的幅度近似相等，用这五年间平均增幅量来估算2015年成年居民年人均阅读图书的数量约为5本；
（3）2014年某小区倾向图书阅读的成年居民有1000人，若该小区2015年与2014年成年居民的人数基本持平，估算2015年该小区成年国民阅读图书的总数量约为7576本．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网