题目内容
1.若一个长方体的体积为(a3-2a2b+ab2)立方厘米,高为(a-b)厘米,则长方体的底面积是a2-ab平方厘米.分析 根据长方体的体积=底面积×高,则长方体底面积=长方体的体积÷高,列出算式,按照整式的乘法即可解答.
解答 解:(a3-2a2b+ab2)÷(a-b)
=a(a2-2ab+b2)÷(a-b)
=a(a-b)2÷(a-b)
=a(a-b)
=a2-ab.
点评 本题考查了整式的除法,解决本题的关键是根据长方体的体积=底面积×高,得到长方体底面积=长方体的体积÷高,列出算式,按照整式的乘法即可解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.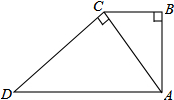 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )| A. | 2:3 | B. | 3:5 | C. | 9:25 | D. | $\sqrt{3}$:$\sqrt{5}$ |
6.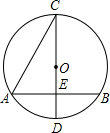 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )| A. | 30° | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | 2 |
8.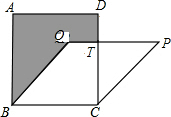 如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
 如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )| A. | 23cm2 | B. | 33cm2 | C. | 43cm2 | D. | 53cm2 |
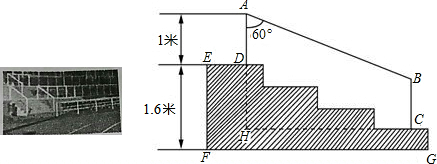
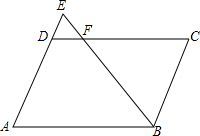 ?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.
?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.