题目内容
18.已知n是一个正整数,若$\sqrt{135n}$与$\sqrt{3}$能合并,则n的最小值是( )| A. | 3 | B. | 5 | C. | 15 | D. | 25 |
分析 根据同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式,可得答案.
解答 解:若$\sqrt{135n}$与$\sqrt{3}$能合并,得
3×45n.45n能开平方,得
n最小值=5,
故选:B.
点评 本题考查同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.

练习册系列答案
相关题目
6.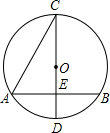 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )| A. | 30° | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | 2 |
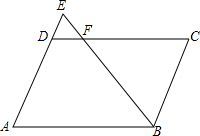 ?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.
?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.