题目内容
 在△ABC中,∠ABC=90°,AC=BC,D是AB上一点,AD=AC,DF⊥AB于D,交BC于F,求证:BD=CF.
在△ABC中,∠ABC=90°,AC=BC,D是AB上一点,AD=AC,DF⊥AB于D,交BC于F,求证:BD=CF.考点:全等三角形的判定与性质,角平分线的性质,等腰直角三角形
专题:证明题
分析:连接AF,易证BD=DF,易证RT△ACF≌RT△ADF,可得CF=DF,即可解题.
解答:证明:连接AF,

∵在△ABC中,∠ABC=90°,AC=BC,
∴∠B=45°,
∵DF⊥AB,
∴BD=DF,
∵在RT△ACF和RT△ADF中,
,
∴RT△ACF≌RT△ADF(HL),
∴CF=DF,
∴BD=CF.

∵在△ABC中,∠ABC=90°,AC=BC,
∴∠B=45°,
∵DF⊥AB,
∴BD=DF,
∵在RT△ACF和RT△ADF中,
|
∴RT△ACF≌RT△ADF(HL),
∴CF=DF,
∴BD=CF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证RT△ACF≌RT△ADF是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 已知,△ABC内接于⊙O,BC是⊙O的直径,点E在⊙O上,OE∥AC,连结AE,若∠AEO=20°,则∠B的度数是
已知,△ABC内接于⊙O,BC是⊙O的直径,点E在⊙O上,OE∥AC,连结AE,若∠AEO=20°,则∠B的度数是 数学小组的同学为了解2014年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将数据进行了整理:
数学小组的同学为了解2014年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将数据进行了整理: 如图,在Rt△ABC中,∠C=90°,点D为AB中点,E、F分别为边BC、AC上两点,且∠EDF=90°
如图,在Rt△ABC中,∠C=90°,点D为AB中点,E、F分别为边BC、AC上两点,且∠EDF=90°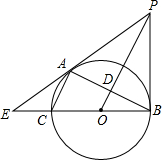 如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E.
如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E. 数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.
数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.