题目内容
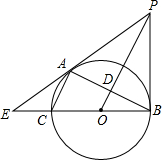如图，已知⊙O是以BC为直径的△ABC的外接圆，OP∥AC，且与BC的垂线交于点P，OP交AB于点D，BC、PA的延长线交于点E．（1）求证：PA是⊙O的切线；
（2）若sinE=
| 3 |
| 5 |
考点：切线的判定,全等三角形的判定与性质
专题：证明题
分析：（1）先利用平行线的性质得到∠ACO=∠POB，∠CAO=∠POA，加上∠ACO=∠CAO，则∠POA=∠POB，于是可根据“SAS”判断△PAO≌△PBO，则∠PAO=∠PBO=90°，然后根据切线的判定定理即可得到PA是⊙O的切线；
（2）先由△PAO≌△PBO得PB=PA=6，在Rt△PBE中，利用正弦的定义可计算PE=10，则AE=PE-PA=4，再在Rt△AOE中，由sinE=
=
，可设OA=3t，则OE=5t，由勾股定理得到AE=4t，则4t=4，解得t=1，所以OA=3；接着在Rt△PBO中利用勾股定理计算出OP=3
，然后证明△EAC∽△EPO，再利用相似比可计算出AC．
（2）先由△PAO≌△PBO得PB=PA=6，在Rt△PBE中，利用正弦的定义可计算PE=10，则AE=PE-PA=4，再在Rt△AOE中，由sinE=
| OA |
| OE |
| 3 |
| 5 |
| 5 |
解答：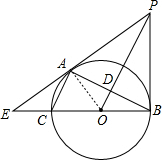
（1）证明：连接OA，如图，
∵AC∥OP，
∴∠ACO=∠POB，∠CAO=∠POA，
又∵OA=OC，
∴∠ACO=∠CAO，
∴∠POA=∠POB，
在△PAO和△PBO中，
，
∴△PAO≌△PBO（SAS），
∴∠PAO=∠PBO，
又∵PB⊥BC，
∴∠PBO=90°，
∴∠PAO=90°，
∴OA⊥PE，
∴PA是⊙O的切线；
（2）解：∵△PAO≌△PBO，
∴PB=PA=6，
在Rt△PBE中，∵sinE=
=
∴
=
，解得PE=10，
∴AE=PE-PA=4，
在Rt△AOE中，sinE=
=
，
设OA=3t，则OE=5t，
∴AE=
=4t，
∴4t=4，解得t=1，
∴OA=3，
在Rt△PBO中，∵OB=3，PB=6，
∴OP=
=3
，
∵AC∥OP，
∴△EAC∽△EPO，
∴
=
，即
=
，
∴AC=
．
（1）证明：连接OA，如图，∵AC∥OP，
∴∠ACO=∠POB，∠CAO=∠POA，
又∵OA=OC，
∴∠ACO=∠CAO，
∴∠POA=∠POB，
在△PAO和△PBO中，
|
∴△PAO≌△PBO（SAS），
∴∠PAO=∠PBO，
又∵PB⊥BC，
∴∠PBO=90°，
∴∠PAO=90°，
∴OA⊥PE，
∴PA是⊙O的切线；
（2）解：∵△PAO≌△PBO，
∴PB=PA=6，
在Rt△PBE中，∵sinE=
| PB |
| PE |
| 3 |
| 5 |
∴
| 6 |
| PE |
| 3 |
| 5 |
∴AE=PE-PA=4，
在Rt△AOE中，sinE=
| OA |
| OE |
| 3 |
| 5 |
设OA=3t，则OE=5t，
∴AE=
| OE2-OA2 |
∴4t=4，解得t=1，
∴OA=3，
在Rt△PBO中，∵OB=3，PB=6，
∴OP=
| OB2+PB2 |
| 5 |
∵AC∥OP，
∴△EAC∽△EPO，
∴
| AC |
| PO |
| EA |
| EP |
| AC | ||
3
|
| 4 |
| 10 |
∴AC=
6
| ||
| 5 |
点评：本题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线．在判定一条直线为圆的切线时，当已知条件中未明确指出直线和圆是否有公共点时，常过圆心作该直线的垂线段，证明该线段的长等于半径；当已知条件中明确指出直线与圆有公共点时，常连接过该公共点的半径，证明该半径垂直于这条直线．也考查了全等三角形的判定与性质．
练习册系列答案
相关题目
在△ABC中，∠ABC=90°，AC=BC，D是AB上一点，AD=AC，DF⊥AB于D，交BC于F，求证：BD=CF．
如图，已知∠C=∠D，∠CAB=∠DBA，AD交BC于点O，请写出图中一组相等的线段
如图，七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G=