Question

如图，在Rt△ABC中，∠C=90°，点D为AB中点，E、F分别为边BC、AC上两点，且∠EDF=90°
（1）求证：AF²+BE²=EF²；
（2）若BE=5，AF=12，求EF的长．

Answer 1

考点：全等三角形的判定与性质,勾股定理,等腰直角三角形

专题：

分析：（1）延长FD到点G，使DG=DF，连接BG，易证EF=EG，△ADF≌△BDG，可得BG=AF，∠DBG=∠A，即可求得∠CBG=90°，即可判定△BEG是直角三角形，根据勾股定理可得BE²+BG²=EG²，即可解题；
（2）根据（1）中结论，将BE、AF的值代入即可求得EF的长．

解答：（1）证明：延长FD到点G，使DG=DF，连接BG，

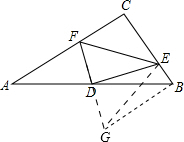
∵∠EDF=90°，DF=DG，
∴DE垂直平分FG，
∴EF=EG，
∵D是AB中点，
∴AD=BD，
在△ADF和△BDG中，

DF=DG ∠ADF=∠BDG AD=BD

，
∴△ADF≌△BDG（SAS），
∴BG=AF，∠DBG=∠A，
∵∠C=90°，
∴∠A+∠ABC=90°，
∴∠CBG=∠ABC+∠DBG=90°，
∴△BEG是直角三角形，
∴BE²+BG²=EG²，
∴AF²+BE²=EF²；
（2）∵AF²+BE²=EF²，BE=5，AF=12，
∴EF²=AF²+BE²=169，
∴EF=13．

点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，考查了直角三角形中勾股定理的运用，本题中求证△ADF≌△BDG是解题的关键．