题目内容
10.下列说法:①若m为任意有理数,则m2+2总是正数;
②方程x+4=$\frac{1}{x}$是一元一次方程;
③若ab>0,a+b<0,则a<0,b<0;
④代数式$\frac{3s}{2}$、$\frac{m+n}{5}$、36、$\frac{2π}{a}$都是整式;
⑤若x2=(-3)2,则x=-3.
其中错误的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 分别根据任意数的偶次方为非负数、一元一次方程定义、有理数的运算法则、整式的定义和平方根的定义判断即可得.
解答 解:①若m为任意有理数,m2≥0,m2+2≥2>0,此结论正确;
②方程x+4=$\frac{1}{x}$的左边$\frac{1}{x}$不是整式,不是一元一次方程,此结论错误;
③若ab>0,则a、b同号,由a+b<0知a<0,b<0,此结论正确;
④代数式$\frac{3s}{2}$、$\frac{m+n}{5}$、36、$\frac{2π}{a}$中$\frac{2π}{a}$是不是整式,此结论错误;
⑤若x2=(-3)2=9,则x=±3,此结论错误;
故选:B.
点评 本题主要考查非负数性质、一元一次方程定义、有理数的运算法则、整式的定义和平方根,掌握基本运算和基本定义是解题的关键.

练习册系列答案
相关题目
20. 图中的两个三角形全等,则∠α=( )
图中的两个三角形全等,则∠α=( )
 图中的两个三角形全等,则∠α=( )
图中的两个三角形全等,则∠α=( )| A. | 72° | B. | 60° | C. | 58° | D. | 50° |
1.下列计算中正确的是( )
| A. | -3-4=-1 | B. | -22-(-2)3=4-8=-4 | C. | $6÷({\frac{1}{2}-\frac{1}{3}})=-6$ | D. | $5×\sqrt{3}-2×\sqrt{3}=3×\sqrt{3}$ |
2. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )
 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )| A. | ②③ | B. | ②④ | C. | ①②③ | D. | ②③④ |
19.已知a,b,c,d为有理数,现规定一种新的运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,那么当$|\begin{array}{l}{2}&{4}\\{(1-x)}&{5x}\end{array}|$=18时,则x的值是( )
| A. | x=1 | B. | $x=\frac{7}{11}$ | C. | $x=\frac{11}{7}$ | D. | x=-1 |
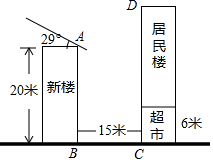 某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)