题目内容
20.若2x-y=$\frac{1}{3}$,xy=2,则2x4y3-x3y4=$\frac{8}{3}$.分析 先把2x4y3-x3y4变形为x3y3(2x-y),再把2x-y=$\frac{1}{3}$,xy=2代入即可.
解答 解:∵2x-y=$\frac{1}{3}$,xy=2,
∴2x4y3-x3y4=x3y3(2x-y)=23×$\frac{1}{3}$=$\frac{8}{3}$;
故答案为:$\frac{8}{3}$.
点评 主要考查了分解因式的实际运用,解此类题目的关键是把2x4y3-x3y4分解为x3y3(2x-y),是一道基础题.

练习册系列答案
相关题目
15.已知mx2yn-1+4x2y9=0,(其中x≠0,y≠0)则m+n=( )
| A. | -6 | B. | 6 | C. | 5 | D. | 14 |
12.若分式$\frac{2xy}{x-3y}$中的x,y的值都变为原来的5倍,则此分式的值( )
| A. | 不变 | B. | 是原来的5倍 | C. | 是原来的$\frac{1}{5}$ | D. | 是原来的$\frac{1}{10}$ |
 如图,D、E分别是BC、AC的中点,BF平分∠ABC交DE于点F,若BC=6,AB=8,则EF的长是1.
如图,D、E分别是BC、AC的中点,BF平分∠ABC交DE于点F,若BC=6,AB=8,则EF的长是1.
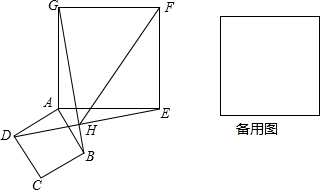 如图,已知正方形ABCD、AEFG边长分别为$\sqrt{2}$cm、2cm,将正方形ABCD绕点A旋转,连接BG、DE相交于点H.
如图,已知正方形ABCD、AEFG边长分别为$\sqrt{2}$cm、2cm,将正方形ABCD绕点A旋转,连接BG、DE相交于点H.