题目内容
2. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )| A. | ②③ | B. | ②④ | C. | ①②③ | D. | ②③④ |
分析 只要证明△ADE≌△ADF,推出AE=EF,DE=DF,推出AD垂直平分线段EF,即可判定②③正确,利用勾股定理即可判定④正确,①不一定成立故错误.
解答 解:∵ AD是△ABC的角平分线,
AD是△ABC的角平分线,
∴∠DAE=∠DAF,
在△ADE和△ADF中,
$\left\{\begin{array}{l}{∠DAE=∠DAF}\\{∠AED=∠AFD=90°}\\{AD=AD}\end{array}\right.$,
∴△ADE≌△ADF,
∴AE=AF,DE=DF,
∴AD垂直平分EF,故②正确,
∵∠EAF=90°时,∠EAF=∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
∵AE=AF,
∴四边形AEDF是正方形,故③正确,
∵AE2+DF2=EO2+AO2+OD2+OF2,
DE2+AF2=OE2+OD2+OA2+OF2,
∴AE2+DF2=AF2+DE2,故④正确,
∵AD垂直平分EF,EF不一定垂直平分AD,故①错误,
故选D.
点评 本题考查正方形的判定、角平分线的性质、全等三角形的判定和性质、线段的垂直平分线的判定、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
12.已知某种型号的纸100张的厚度约为1cm,那么这种型号的纸13亿张的厚度约为( )
| A. | 1.3×105km | B. | 1.3×104km | C. | 1.3×103km | D. | 1.3×102km |
7.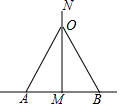 如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)
如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)
 如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)
如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)| A. | 14m | B. | 11m | C. | 13m | D. | 10m |
12.若分式$\frac{2xy}{x-3y}$中的x,y的值都变为原来的5倍,则此分式的值( )
| A. | 不变 | B. | 是原来的5倍 | C. | 是原来的$\frac{1}{5}$ | D. | 是原来的$\frac{1}{10}$ |
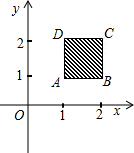 如图,在平面直角坐标系中,我们把正方形ABCD称为黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=-2x+b发射信号,当信号遇到黑色区域时,黑色区域便由黑变白,则能够使黑色区域由黑变白的b的取值范围是3≤b≤6.
如图,在平面直角坐标系中,我们把正方形ABCD称为黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=-2x+b发射信号,当信号遇到黑色区域时,黑色区域便由黑变白,则能够使黑色区域由黑变白的b的取值范围是3≤b≤6.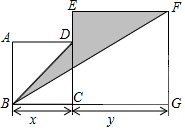 如图:四边形ABCD和四边形ECGF都是正方形,其边长分别为x、y(点B、C、G和点C、D、E分别在一条直线上)则图中阴影部分的面积为:$\frac{1}{2}{x}^{2}-\frac{1}{2}xy+\frac{1}{2}{y}^{2}$(用含x、y的代数式表示,且按x降幂排列)
如图:四边形ABCD和四边形ECGF都是正方形,其边长分别为x、y(点B、C、G和点C、D、E分别在一条直线上)则图中阴影部分的面积为:$\frac{1}{2}{x}^{2}-\frac{1}{2}xy+\frac{1}{2}{y}^{2}$(用含x、y的代数式表示,且按x降幂排列) 如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=$\frac{1}{3}$.
如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=$\frac{1}{3}$.