题目内容
在图示的四个汽车标志图案中，能用平移变换来分析其形成过程的图案是( )
A. 
B. 
C. 
D. 
D
【解析】试题分析：根据平移的概念，即平移前后图形的大小，形状都不变，只是位置改变.
故选D.
练习册系列答案
相关题目
一堆有红、白两种颜色的球若干个，已知白球的个数比红球少，但白球的2倍比红球多．若把每一个白球都记作“2”，每一个红球都记作“3”，则总数为“60”，那么这两种球各有多少个？
白球有9个，红球有14个．
【解析】【试题分析】设白球有x个，红球有y个，根据“白球的个数比红球少，但白球的2倍比红球多”，得 ，解得7.5＜x＜12，则x可以取8,9,10,11.
由于2x=60－3y=3（20－y） 得2x应是3的倍数，则x只能取9，y = = 14
即白球有9个，红球有14个．
【试题解析】
设白球有x个，红球有y个，由题意，得
由第一个... 如图所示，l1，l2，l3交于点O，∠1＝∠2，∠3∶∠1＝8∶1，求∠4的度数．
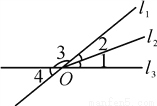
∠4＝36°
【解析】试题分析：设∠1=x，根据题意表示出∠2，再表示出∠3，然后根据邻补角的和等于180°列式求出x，再根据对顶角相等求出∠4即可．
【解析】
设∠1=x，则∠2=x，∠3=8x，依题意有
x+x+8x=180°，
解得x=18°，
则∠4=18°+18°=36°．
故∠4的度数是36°． 如图，点Ａ，Ｏ，Ｂ在同一直线上，已知∠BOC=50°，则∠AOC=__________.
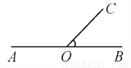
130°
【解析】因为∠BOC=50°,所以∠AOC=180°－∠BOC=180°－50°=130°,故答案为:130°. 已知一副直角三角板如图放置，其中BC＝3，EF＝4，把30°的三角板向右平移，使顶点B落在45°的三角板的斜边DF上，则AE＝ _________.
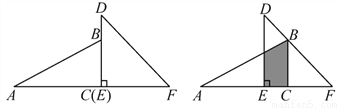
3－1
【解析】试题分析：∵∠F＝45°，BC＝3，
∴CF＝3，又EF＝4，
则EC＝1，
∵BC＝3，∠A＝30°，
∴AC＝，
则AE＝－1．
故答案为： －1． 已知∠A为锐角，求满足下列条件的∠A度数．
（1）sinA=0.9816；
（2）tanA=0.1890
（1）79°；（2）11°
【解析】试题分析：（1）正确使用计算器计算即可．使用2nd键，然后按sin-1 0.9816即可求出∠A的度数；（2）使用2nd键，然后按tan-1 0.1890即可求出∠A的度数．
试题解析：
【解析】
（1）∵sinA=0.9816，∴∠A≈79°；
（2）∵tanA=0.1890，∴∠A≈11°． 四位学生用计算器求sin62°20′的值正确的是（ ）
A. 0.8857 B. 0.8856 C. 0.8852 D. 0.8851
A
【解析】试题解析：
故选A. 如图，直线AB，CD相交于点O，OE平分∠BOD，∠AOC=72°，∠DOF=90°．
(1) 写出图中任意一对互余的角；
(2) 求∠EOF的度数．
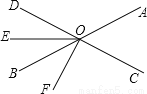
（1）∠BOF和∠BOD互余；（2）54°
【解析】试题分析：（1）根据两角互余的性质得出互余的角；（2）首先根据题意得出∠COF=90°，根据∠AOC的度数得出∠BOF和∠BOD的度数，根据角平分线的性质得出∠BOE的度数，从而根据∠EOF=∠BOF+∠BOE得出答案．
试题解析：（1）∠BOF与∠BOD或∠DOE与∠EOF
（2）∵∠COF＝180°－∠DOF＝90°， ∴∠... 满足－2x＞－12的非负整数有________________________．
0，1，2，3，4，5
【解析】∵不等式-2x＞-12的解为x＜6，∴满足x＜6的非负整数有0，1，2，3，4，5．