题目内容
如图，直线AB，CD相交于点O，OE平分∠BOD，∠AOC=72°，∠DOF=90°．
(1) 写出图中任意一对互余的角；
(2) 求∠EOF的度数．
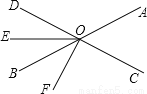
（1）∠BOF和∠BOD互余；（2）54°
【解析】试题分析：（1）根据两角互余的性质得出互余的角；（2）首先根据题意得出∠COF=90°，根据∠AOC的度数得出∠BOF和∠BOD的度数，根据角平分线的性质得出∠BOE的度数，从而根据∠EOF=∠BOF+∠BOE得出答案．
试题解析：（1）∠BOF与∠BOD或∠DOE与∠EOF
（2）∵∠COF＝180°－∠DOF＝90°， ∴∠...
阅读快车系列答案如图是数轴的一部分,其单位长度为a,已知在△ABC中,AB=3a,BC=4a,AC=5a.用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法).
见解析
【解析】【试题分析】利用“SSS”作出三角形，作图方法见解析.
【试题解析】
如图.
作法如下:
(1)在数轴上截取AC=5a.
(2)分别以A,C为圆心,以3a,4a为半径画弧,两弧相交于点B.
(3)连接AB,BC,则△ABC即为所求作的三角形. 在图示的四个汽车标志图案中，能用平移变换来分析其形成过程的图案是( )
A. 
B. 
C. 
D. 
D
【解析】试题分析：根据平移的概念，即平移前后图形的大小，形状都不变，只是位置改变.
故选D. 用科学记算器算得①293=24389；②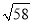
≈7.615773106；③sin35°≈0.573576436；④若tana=5，则锐角a≈0.087488663°．其中正确的是（ ）
A. ①②③ B. ①②④ C. ②③④ D. ①③④
A
【解析】试题分析：①②③利用计算器计算可得是正确的，
④tan45°=1，tana=5，说明α的度数应大于45°，所以错误，
故选A． 下面四个数中，最大的是（ ）
A.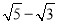 
B. sin88° C. tan46° D.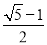 
C
【解析】试题分析：A、≈2.236-1.732≈0.504；
B、sin88°≈0.999；
C、tan46°≈1.036；
D、 ≈ ≈0.568．
故tan46°最大，
故选：C． 小明从A地出发行走到B地,并从B地返回到A地,同时小张从B地骑车匀速到达A地后,发现忘带东西,立刻以原速返回取到东西后,再以原速赶往A地,结果与小明同时到达A地,如图为小明离A地距离s(单位:km)与所用时间t(单位:h)之间关系,则小明与小张第2次相遇时离A地_____km.
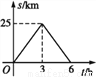
20
【解析】【解析】
小明的速度=km/h，小张的速度==km/h，设小明与小张第2次相遇时经历时间为t，由题意得： t+t=25×3，解得：t=，则此时小明离A地的距离=25﹣×（﹣3）=20km．故答案为：20． 有一游泳池注满水,现按一定速度将水排尽,然后进行清洗,再按相同速度注满清水,使用一段时间后,又按相同的速度将水排尽,则游泳池的存水量V(m3)随时间t(h)变化的大致图象是( )
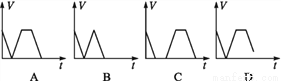
C
【解析】【解析】
根据题意分析可得：存水量V的变化有几个阶段：
1、减小为0，并持续一段时间；
2、增加至最大，并持续一段时间；
3、减小为0．
故选A． 根据已知条件写出相应不等式．
(1)－3，－2，－1,0,1都是不等式的解；
(2)不等式的负整数解只有－1，－2，－3；
(3)不等式的解的最大的值是0.
见解析
【解析】分析：根据题中的条件，得出每个小题中的数据在不等式的解集范围内即可.
本题解析：
(1)∵不等式有五个连续的整数解，
∴求不等式x-1≤0的五个最大整数解。
(2)∵不等式有三个连续的负整数解
∴求不等式2(x+1) ≤0的三个最大负整数解。
(3)∵不等式的解的最大的值是0，
∴求不等式x-1<0的最大整数解。 如图，在等边△ABC中，P为△ABC内任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，AM⊥BC于M，试猜想AM、PD、PE、PF之间的关系，并说明你的猜想．
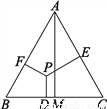
AM＝PD＋PE＋PF，理由见解析
【解析】试题分析：连接AP、BP、CP，根据面积相等，又利用△ABC是等边三角形，即可得PE+PD+PF=AM.
试题解析：PE+PD+PF=AM，理轴如下：
连接AP、BP、CP，
∵S△ABP+S△BCP+S△ACP=S△ABC，
∴AB×PE+BC×PD+AC×PF＝BC×AM，
∵△ABC是等边三角形，
∴AB=...