题目内容
18.(1)解分式方程:$\frac{1}{x-2}-\frac{4}{{{x^2}-4}}$=1(2)计算:-80+($\frac{1}{3}$)-1+$\frac{2}{\sqrt{3}-1}$+|1-tan60°|
分析 (1)先把方程两边同乘以(x+2)(x-2)得到整式方程x+2-4=x2-4,再解此整式方程,然后进行检验确定原方程的解;
(2)根据零指数幂、负整数整数幂和特殊角的三角函数值得到原式=-1+3+$\sqrt{3}$+1+|1-$\sqrt{3}$|,然后去绝对值后合并即可.
解答 解:(1)去分母得x+2-4=x2-4,
整理得x2-x-2=0,解得x1=2,x2=-1,
检验:当x=2时,(x+2)(x-2)=0,则x=2是原方程的增根;x=-1时,(x+2)(x-2)≠0,
所以原方程的解为x=-1;
(2)原式=-1+3+$\sqrt{3}$+1+|1-$\sqrt{3}$|
=-1+3+$\sqrt{3}$+1+$\sqrt{3}$-1
=2$\sqrt{3}$+4.
点评 本题考查了二次根式的混合计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了解分式方程.

练习册系列答案
相关题目
13.不等式组$\left\{\begin{array}{l}2x+5≤3(x+2)\\ \frac{x-1}{2}<\frac{1}{3}\end{array}\right.$的整数解的个数为( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
3.为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:
(说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费)已知小明家2014年4月份用水20吨,交水费66元;5月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民6月用水27吨,其当月交水费多少元?
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民6月用水27吨,其当月交水费多少元?
7.计算[-2(-xn-1)]3=( )
| A. | -2x3n-1 | B. | 8x3n-3 | C. | 16x3n-3 | D. | -16x3n-3 |
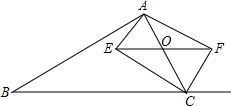 如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
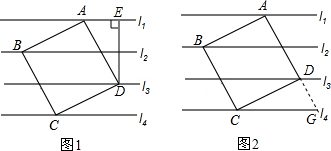
如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F 如图,在?ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连结AE、AF.
如图,在?ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连结AE、AF.