题目内容
9.如图1,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点A、B、C、D分别在l1、l2、l3、l4上,过点D作DE⊥l1于点E.已知相邻两条平行线之间的距离为2.(1)求AE及正方形ABCD的边长;
(2)如图2,延长AD交l4于点G,求CG的长度.
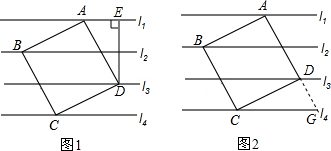
分析 (1)利用已知得出△FAB≌△EDA(AAS),即可得出AE,以及正方形的边长;
(2)如图2,过点D作DH⊥CG于点H,利用勾股定理求得DH的长度,然后由射影定理来求CG的长度.
解答 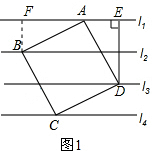 解:(1)如图1,过B点作BF⊥l1,垂足为F,
解:(1)如图1,过B点作BF⊥l1,垂足为F,
∵∠FAB+∠EAD=90°,∠FAB+∠FBA=90°,
∴∠FBA=∠EAD,
在△FAB与△EDA中,
$\left\{\begin{array}{l}{∠BFA=∠AED}\\{∠FBA=∠EAD}\\{AB=DA}\end{array}\right.$,
∴△FAB≌△EDA(AAS),
∴AE=BF=2,ED=4,
∴AD=2$\sqrt{5}$;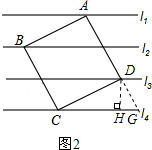
(2)如图2,过点D作DH⊥CG于点H,
∵CD=AD=2$\sqrt{5}$,DH=2,
∴CH=$\sqrt{C{D}^{2}-D{H}^{2}}$=4,
∵CD2=CH•CG,
∴20=4CG,则CG=5.
点评 此题主要考查了勾股定理以及全等三角形的判定与性质等知识,熟练应用全等三角形的判定方法是解题关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
20.太阳的半径约为696000千米,用科学记数法可表示为( )
| A. | 6.96×103千米 | B. | 6.96×104千米 | C. | 6.96×105千米 | D. | 6.96×106千米 |
14.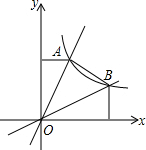 如图,两个正比例函数y=k1x(k1>0),y=k2x(k2>0)的图象与反比例函数y=$\frac{1}{x}$的图象在第一象限分别相交于A、B两点.已知k1≠k2,OA=OB,则k1k2的值为( )
如图,两个正比例函数y=k1x(k1>0),y=k2x(k2>0)的图象与反比例函数y=$\frac{1}{x}$的图象在第一象限分别相交于A、B两点.已知k1≠k2,OA=OB,则k1k2的值为( )
 如图,两个正比例函数y=k1x(k1>0),y=k2x(k2>0)的图象与反比例函数y=$\frac{1}{x}$的图象在第一象限分别相交于A、B两点.已知k1≠k2,OA=OB,则k1k2的值为( )
如图,两个正比例函数y=k1x(k1>0),y=k2x(k2>0)的图象与反比例函数y=$\frac{1}{x}$的图象在第一象限分别相交于A、B两点.已知k1≠k2,OA=OB,则k1k2的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
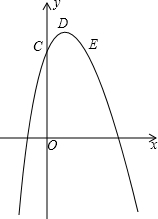 如图,已知抛物线的顶点坐标为D(1,5),抛物线与y轴交于点C(0,4),点C和点E关于对称轴对称.
如图,已知抛物线的顶点坐标为D(1,5),抛物线与y轴交于点C(0,4),点C和点E关于对称轴对称.