题目内容
18．十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：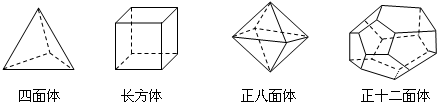
（1）根据上面多面体模型，完成表格中的空格：
| 多面体 | 顶点数（V） | 面数（F） | 棱数（E） |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
（3）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是20．
分析 （1）观察图形即可得出结论；
（2）观察可得顶点数+面数-棱数=2；
（3）代入（2）中的式子即可得到面数．
解答 解：（1）观察图形，四面体的棱数为6；正八面体的顶点数为6；正十二面体的面数为12；
（2）观察表格可以看出：顶点数+面数-棱数=2，关系式为：V+F-E=2；
（3）由题意得：F-8+F-30=2，解得F=20．
故答案为：（1）6，6，12；（2）V+F-E=2；（3）20．
点评 本题考查多面体的顶点数，面数，棱数之间的关系及灵活运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．数1，$\frac{3}{4}$，$\frac{5}{9}$，$\frac{7}{16}$，$\frac{9}{25}$…按此规律写下去，那么第n（n为正整数）个数是（ ）
| A． | $\frac{2n+1}{{n}^{2}}$ | B． | $\frac{2n-1}{n}$ | C． | $\frac{2n-1}{{n}^{2}}$ | D． | $\frac{n-4}{{n}^{2}}$ |
6．在实数范围内，下列各式一定有意义的是（ ）
| A． | $\sqrt{{a}^{2}-1}$ | B． | $\sqrt{a}$ | C． | $\sqrt{2a+1}$ | D． | $\sqrt{{a}^{2}+0.1}$ |
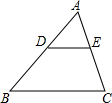如图，已知D、E分别是的AB、AC边上的点，DE∥BC，且AE：EC=2：5，那么S△ADE：S四边形DBCE等于4：21．
如图，已知AB∥CD∥EF，∠x=80°，∠z=25°，则∠y=125°．