题目内容
3．
如图，已知AB∥CD∥EF，∠x=80°，∠z=25°，则∠y=125°．
分析 先根据AB∥CD，∠x=80°，∠z=25°得出∠CEF的度数，再由CD∥EF即可得出∠y的度数．
解答 解：∵AB∥CD，∠x=80°，∠z=25°，
∴∠z+∠CEF=∠x=80°，
∴∠CEF=80°-25°=55°．
∵CD∥EF，
∴∠y=180°-55°=125°．
故答案为：125°．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．
练习册系列答案
阅读快车系列答案
相关题目
18．十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：
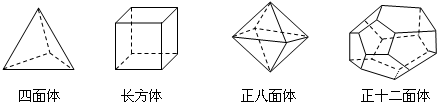
（1）根据上面多面体模型，完成表格中的空格：
（2）你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是V+F-E=2．
（3）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是20．
（1）根据上面多面体模型，完成表格中的空格：
| 多面体 | 顶点数（V） | 面数（F） | 棱数（E） |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
（3）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是20．
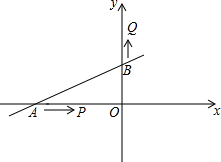直线y=$\frac{1}{2}$x+2交x轴于A，交y轴于B，P点从A点出发沿射线AO运动，同时Q从B点出发沿射线OB方向运动，速度均为1个单位/秒
如图，∠A=29°，∠C′=62°，△ABC与△A′B′C′关于直线l对称，则∠B=89°．
如图，已知△ABC中，AD是∠BAC的平分线，AD又是BC边上的中线，求证：△ABC是等腰三角形．