题目内容
13.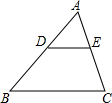 如图,已知D、E分别是的AB、AC边上的点,DE∥BC,且AE:EC=2:5,那么S△ADE:S四边形DBCE等于4:21.
如图,已知D、E分别是的AB、AC边上的点,DE∥BC,且AE:EC=2:5,那么S△ADE:S四边形DBCE等于4:21.
分析 由DE∥BC可判断△ADE∽△ABC,根据相似三角形面积的比等于相似比的平分得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{4}{25}$,然后利用比例的性质即可得到S△ADE与S四边形DBCE的比值.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AE}{AC}$)2=($\frac{2}{5}$)2=$\frac{4}{25}$,
∴S△ADE:S四边形DBCE=4:21.
故答案为4:21.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;相似三角形面积的比等于相似比的平分.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
18.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
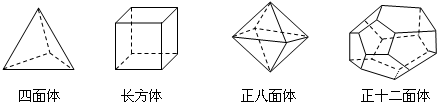
(1)根据上面多面体模型,完成表格中的空格:
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2.
(3)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是20.

(1)根据上面多面体模型,完成表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
(3)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是20.
5.下列说法中正确的是( )
| A. | 已知a,b,c是三角形的三边长,则a2+b2=c2 | |
| B. | 在直角三角形中,两边长和的平方等于第三边长的平方 | |
| C. | 在Rt△ABC中,若∠C=90°,则三角形对应的三边满足a2+b2=c2 | |
| D. | 在Rt△ABC中,若∠A=90°,则三角形对应的三边满足a2+b2=c2 |
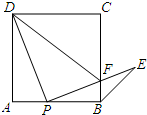 如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.
如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.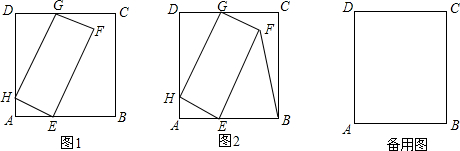
 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是多少元(结果保留整数).
如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是多少元(结果保留整数).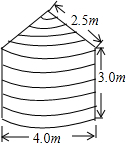 如图,要造一个粮仓,其上部是圆锥形,下部是圆柱形,如果每平方米需要用铁皮2m2(底部不用铁皮,接头忽略不计),那么按图中尺寸计算,一共需要多少平方米铁皮?(精确到0.1m2)
如图,要造一个粮仓,其上部是圆锥形,下部是圆柱形,如果每平方米需要用铁皮2m2(底部不用铁皮,接头忽略不计),那么按图中尺寸计算,一共需要多少平方米铁皮?(精确到0.1m2)