��Ŀ����
10������˵������$\sqrt{6}$�Ƕ��θ�ʽ����������ʽ��
�ڷ���x2-x-k=0�ĸ�Ϊx=$\frac{1+\sqrt{1+4k}}{2}$��
����ac��0����ax2+bx+c=0������������ȵ�ʵ������
����ѧ�α���41ҳ�۲������������һԪ���η��̸���ϵ���Ĺ�ϵ��������һ��ϵ�÷���x2-3x+5=0����������3����������5��
���д�����Т٢ڢܣ�
���� �ֱ�������ʽ�Ķ����Լ����ݸ���ϵ���Ĺ�ϵ�����б�ʽ�ֱ��жϵó����ɣ�
��� �⣺��$\sqrt{6}$�Ƕ��θ�ʽ��Ҳ����ʽ���ʴ�ѡ����������⣻
�ڷ���x2-x-k=0����b2-4ac��0ʱ�����̵ĸ�Ϊx=$\frac{1��\sqrt{1+4k}}{2}$���ʴ�ѡ����������⣻
����ac��0����ax2+bx+c=0�У�b2-4ac��0���ʷ��̱�����������ȵ�ʵ��������ȷ���������⣻
����ѧ�α���41ҳ�۲������������һԪ���η��̸���ϵ���Ĺ�ϵ��
������һ��ϵ����x2-3x+5=0����b2-4ac=9-20=-11�������ø���ϵ����ϵ���ʴ�ѡ����������⣮
���д�����У��٢ڢܣ�
�ʴ�Ϊ���٢ڢܣ�
���� ������Ҫ��������ʽ�Ķ����Լ�������ϵ���Ĺ�ϵ�����б�ʽ��֪ʶ����ȷ���ո�����ϵ���Ĺ�ϵ�ǽ���ؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
20������2-x��$\sqrt{\frac{1}{x-2}}$���������ʽ�Ƶ������ڣ��ã�������
| A�� | $\sqrt{x-2}$ | B�� | $\sqrt{2-x}$ | C�� | -2$\sqrt{2-x}$ | D�� | -$\sqrt{x-2}$ |
18��ʮ��������ʿ��ѧ��ŷ��֤���˼������ж�������V����������F����������E��֮����ڵ�һ����Ȥ�Ĺ�ϵʽ������Ϊŷ����ʽ������۲����м��ּ�����ģ�ͣ�����������⣺
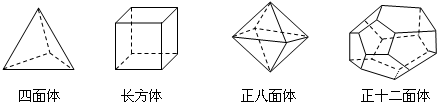
��1���������������ģ�ͣ���ɱ����еĿո�
��2���㷢�ֶ�������V����������F����������E��֮����ڵĹ�ϵʽ��V+F-E=2��
��3��һ��������������ȶ�������8������30���⣬������������������20��

��1���������������ģ�ͣ���ɱ����еĿո�
| ������ | ��������V�� | ������F�� | ������E�� |
| ������ | 4 | 4 | 6 |
| ������ | 8 | 6 | 12 |
| �������� | 6 | 8 | 12 |
| ��ʮ������ | 20 | 12 | 30 |
��3��һ��������������ȶ�������8������30���⣬������������������20��
5������˵������ȷ���ǣ�������
| A�� | ��֪a��b��c�������ε����߳�����a2+b2=c2 | |
| B�� | ��ֱ���������У����߳��͵�ƽ�����ڵ����߳���ƽ�� | |
| C�� | ��Rt��ABC�У�����C=90�㣬�������ζ�Ӧ����������a2+b2=c2 | |
| D�� | ��Rt��ABC�У�����A=90�㣬�������ζ�Ӧ����������a2+b2=c2 |
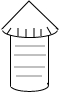 ��ͼ�����ֵĶ�����Բ��״�����Բ����Բ�İ뾶��Ϊ3m��ĸ�߳�Ϊ6m��Ϊ��ֹ��ˮ���������ֶ���������ձ�������ձ���г�����ÿƽ����10ԪǮ����ô������ձ����Ҫ�ķ����Ƕ���Ԫ�����������������
��ͼ�����ֵĶ�����Բ��״�����Բ����Բ�İ뾶��Ϊ3m��ĸ�߳�Ϊ6m��Ϊ��ֹ��ˮ���������ֶ���������ձ�������ձ���г�����ÿƽ����10ԪǮ����ô������ձ����Ҫ�ķ����Ƕ���Ԫ�����������������


