题目内容
10.计算:(1)2$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{3}}$+$\sqrt{8}$
(2)2$\sqrt{10}$×$3\sqrt{5}$-4$\sqrt{2}$
(3)(3$\sqrt{48}$-2$\sqrt{27}$)$÷\sqrt{3}$
(4)$\sqrt{1\frac{2}{3}}÷\sqrt{2\frac{1}{3}}×\sqrt{1\frac{2}{5}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先进行二次根式的乘法运算,然后化简后合并即可;
(3)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算;
(4)根据二次根式的乘除法则运算.
解答 解:(1)原式=$\sqrt{2}$-2$\sqrt{3}$+2$\sqrt{2}$
=3$\sqrt{2}$-2$\sqrt{3}$;
(2)原式=6$\sqrt{10×5}$-4$\sqrt{2}$
=30$\sqrt{2}$-4$\sqrt{2}$
=26$\sqrt{2}$;
(3)原式=(12$\sqrt{3}$-6$\sqrt{3}$)÷$\sqrt{3}$
=6$\sqrt{3}$÷$\sqrt{3}$
=6;
(4)原式=$\sqrt{\frac{5}{3}•\frac{3}{7}•\frac{7}{5}}$
=1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20. 如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
 如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )| A. | 36° | B. | 120° | C. | 38° | D. | 76° |
19.如果菱形的边长是α,一个内角是60度,那么菱形较短的对角线长等于( )
| A. | $\frac{1}{2}α$ | B. | $\frac{{\sqrt{3}}}{2}a$ | C. | a | D. | $\sqrt{3a}$ |
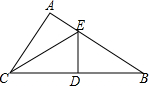 如图,在Rt△ABC中,∠A=90°,边BC的垂直平分线DE交AB于点E,连接CE.求证:BE2=AC2+AE2.
如图,在Rt△ABC中,∠A=90°,边BC的垂直平分线DE交AB于点E,连接CE.求证:BE2=AC2+AE2.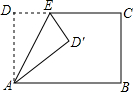 将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.
将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.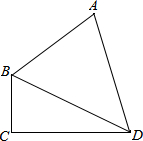 如图,四边形ABCD中,已知AB=10,CD=12,对角线BD平分∠ABC,∠ADB=45°,∠BCD=90°,则边BC的长度为4或6.
如图,四边形ABCD中,已知AB=10,CD=12,对角线BD平分∠ABC,∠ADB=45°,∠BCD=90°,则边BC的长度为4或6.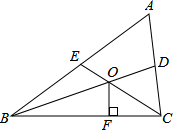 如图,△ABC 的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=4,OF=3,则四边形ADOE的面积是7.5.
如图,△ABC 的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=4,OF=3,则四边形ADOE的面积是7.5.