题目内容
1.对于三个数a、b、c,M{a,b,c}表示a,b,c这三个数的平均数,min{a,b,c}表示a、b、c这三个数中最小的数,如:M$\left\{{-1\;,\;2\;,\;3}\right\}=\frac{-1+2+3}{3}=\frac{4}{3}$,min{-1,2,3}=-1;M$\left\{{-1\;,\;2\;,\;a}\right\}=\frac{-1+2+a}{3}=\frac{a+1}{3}$,min$\left\{{-1\;,\;2\;,\;a}\right\}=\left\{\begin{array}{l}a({a≤-1})\\-1({a>-1})\end{array}$.解决下列问题:
(1)填空:若min{2,2x+2,4-2x}=2,则x的取值范围是0≤x≤1;
(2)①若M{2,x+1,2x}=min{2,x+1,2x},那么x=1;
②根据①,你发现结论“若M{a,b,c}=min{a,b,c},那么a=b=c”(填a,b,c大小关系);
③运用②,填空:若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=-4.
分析 结合题意,分情况讨论,将实际问题与数学思想联系起来,读懂题列出算式或一元一次不等式组即可求解.
解答 解:(1)由题意得:
$\left\{\begin{array}{l}{2x+2≥2}\\{4-2x≥2}\end{array}\right.$,
求解得:0≤x≤1.
(2)①M{2,x+1,2x}=$\frac{2+x+1+2x}{3}$=x+1.
法一:当x≥1时,则min{2,x+1,2x}=2,则x+1=2,x=1.
当x<1时,则min{2,x+1,2x}=2x,则x+1=2x,x=1(舍去).
综上所述:x=1.
法二:∵M{2,x+1,2x}=}=$\frac{2+x+1+2x}{3}$=x+1=min{2,x+1,2x},
∴$\left\{\begin{array}{l}{2≥x+1}\\{2x≥x+1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x≤1}\\{x≥1}\end{array}\right.$,
∴x=1.
②由①可知:a=b=c;
③由②可知:2x+y+2=2x-y,则y=-1,
x+2y=2x-y,x=-3,
所以x+y=-4.
故答案为:(1)0≤x≤1;(2)①1,②a=b=c,③-4.
点评 此题考查解不等式与不等式组,解决问题的关键是读懂题意,依题意列出不等式进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若ax=3,ay=2,则a2x-y等于( )
| A. | 8 | B. | $\frac{9}{2}$ | C. | 11 | D. | 7 |
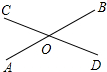 如图,直线AB与CD相交于点O,∠AOC:∠COB=2:3,则∠BOD=72°.
如图,直线AB与CD相交于点O,∠AOC:∠COB=2:3,则∠BOD=72°.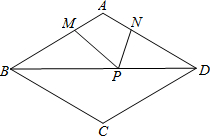 如图,在菱形ABCD中,AB=6,∠ABC=60°,点M、N分别在AB、AD边上,AM=AN=2,P是对角线BD上的动点,则PM+PN的最小值是2$\sqrt{7}$.
如图,在菱形ABCD中,AB=6,∠ABC=60°,点M、N分别在AB、AD边上,AM=AN=2,P是对角线BD上的动点,则PM+PN的最小值是2$\sqrt{7}$.