题目内容
11.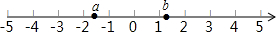 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
分析 根据数轴上点的位置关系,可得a、b的大小,根据非负数的性质,可化简整式,根据整式的加减,可得答案.
解答 解:由a、b位于数轴上的位置,得
-2<a<-1,1<b<1.5,
原式=-a-1+2(b-1)-(b-a)
=-a-1+2b-2-b+a
=b-3.
点评 本题考查了实数与数轴,利用数轴上点的位置关系得出a、b的大小是解题关键.

练习册系列答案
相关题目
 已知在平面直角坐标系中,已知A(3,4),B(3,-1),C(-3,-2),D(-2,3)
已知在平面直角坐标系中,已知A(3,4),B(3,-1),C(-3,-2),D(-2,3)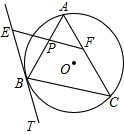 如图,△ABC是⊙O的内接三角形,BT是⊙O的切线,P是线段AB上一点,经过P作BC的平行线与BT交于E点,与AC交于F点.
如图,△ABC是⊙O的内接三角形,BT是⊙O的切线,P是线段AB上一点,经过P作BC的平行线与BT交于E点,与AC交于F点. 如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D,
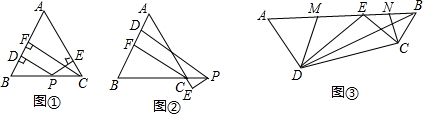
如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D, 如图,点P是等腰Rt△ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设点D为BC中点,求证:△DEF是等腰直角三角形.
如图,点P是等腰Rt△ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设点D为BC中点,求证:△DEF是等腰直角三角形.