题目内容
2．先化简，再求值：（$\frac{a-1}{a}$-$\frac{a-2}{a+1}$）÷$\frac{2{a}^{2}-a}{{a}^{2}+2a+1}$．其中a满足等式2a2-3a-3=0．分析 先把括号内通分，再把分子分母因式分解，接着把除法运算化为乘法运算，约分后化简，然后把2a2-3a-3=0变形得到a2=$\frac{3}{2}$（a+1），再利用整体代入的方法计算．
解答 解：原式=$\frac{（a-1）（a+1）-a（a-2）}{a（a+1）}$÷$\frac{a（2a-1）}{（a+1）^{2}}$
=$\frac{2a-1}{a（a+1）}$•$\frac{（a+1）^{2}}{a（2a-1）}$
=$\frac{a+1}{{a}^{2}}$
∵2a2-3a-3=0，
∴a2=$\frac{3}{2}$（a+1），
∴原式=$\frac{2}{3}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
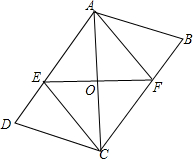如图．四边形ABCD中，AB=CD，AD=BC，对角线AC的中点为O，过点O的直线分别交AD、BC于点E、F．
如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AB=10，EF=2，求AH的长．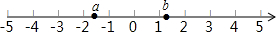
已知：实数a，b在数轴上的位置如图所示，化简：$\sqrt{（a+1）^{2}}$+2$\sqrt{（b-1）^{2}}$-|a-b|．