题目内容
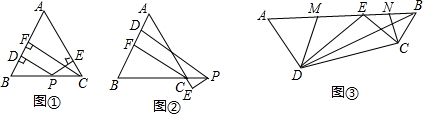
1.我们把过等腰三角形的底边所在的直线上的点作两腰的垂线及作一腰的高的图形称为“腰垂等腰三角形”,如图①,图②,在△ABC中,AB=AC,点P为边BC(或BC所在的直线)上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F.像这样的图形就称为“腰垂等腰三角形”.特例探索
(1)如图①,若PD=5,PE=3,则CF=8;如图①,若PD=6,PE=4,则CF=10;
变式探究
(2)如图②,当点P在BC延长线上时,其余条件不变,猜想PD,PE,CF的数量关系,并给出证明:
拓展应用
(3)图③是一个航模的截面示意图,在四边形ABCD中,点E为AB边上的一点,ED⊥AD,EC⊥AB,垂足分别为D,C,且AD•CE=DE•BC,AB=2$\sqrt{13}$dm,AD=3dm,BD=$\sqrt{37}$dm.点M,N分别为AE,BE的中点,连接DM,CN,求△DEM与△CEN的周长之和.
分析 (1)连接AP,如图①,只需运用面积法就可得到CF、PD、PE三者之间的关系,就可解决问题;
(2)连接AP,如图②,只需运用面积法就可解决问题;
(3)由条件AD•CE=DE•BC联想到三角形相似,从而得到∠A=∠ABC,进而补全等腰三角形,△DEM与△CEN的周长之和就可转化为AB+BH,而BH是△ADB的边AD上的高,只需利用勾股定理建立方程,求出DH,再求出BH,就可解决问题.
解答 解:(1)连接AP,如图①.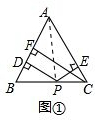
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP+S△ACP,
∴$\frac{1}{2}$AB•CF=$\frac{1}{2}$AB•PD+$\frac{1}{2}$AC•PE.
∵AB=AC,
∴CF=PD+PE.
∴当PD=5,PE=3时,CF=5+3=8;当PD=6,PE=4时,CF=6+4=10.
故答案为8,10;
(2)CF=PD-PE.
理由如下:连接AP,如图②.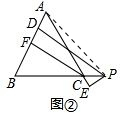
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP-S△ACP,
∴$\frac{1}{2}$AB•CF=$\frac{1}{2}$AB•PD-$\frac{1}{2}$AC•PE.
∵AB=AC,
∴CF=PD-PE.
(3)延长AD、BC交于点F,作BH⊥AF,垂足为H,如图③.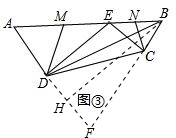
∵AD•CE=DE•BC,
∴$\frac{AD}{DE}=\frac{BC}{EC}$.
∵ED⊥AD,EC⊥CB,
∴∠ADE=∠BCE=90°.
∴△ADE∽△BCE.
∴∠A=∠CBE.
∴FA=FB.
同(1)得ED+EC=BH.
设DH=xdm,
则AH=AD+DH=(3+x)dm.
∵BH⊥AF,
∴∠BHA=90°.
∴BH2=BD2-DH2=AB2-AH2.
∵AB=2$\sqrt{13}$,AD=3,BD=$\sqrt{37}$,
∴($\sqrt{37}$)2-x2=(2$\sqrt{13}$)2-(3+x)2.
解得:x=1.
∴BH2=BD2-DH2=37-1=36.
∴BH=6dm.
∴ED+EC=6.
∵∠ADE=∠BCE=90°,
且M、N分别为AE、BE的中点,
∴DM=AM=EM=$\frac{1}{2}$AE,CN=BN=EN=$\frac{1}{2}$BE.
∴△DEM与△CEN的周长之和=DE+DM+EM+CN+EN+EC
=DE+AE+BE+EC=DE+AB+EC
=DE+EC+AB
=6+2$\sqrt{13}$.
∴△DEM与△CEN的周长之和为(6+2$\sqrt{13}$)dm.
点评 本题考查了等腰三角形的性质与判定、相似三角形的性质与判定、直角三角形斜边上的中线等于斜边的一半、勾股定理等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力.

| A. | x≥0 | B. | x>-1 | C. | x≥-1 | D. | x≥1 |
| A. | $\sqrt{x-1}=-1$ | B. | $\sqrt{x-1}=x$ | C. | x2+mx-1=0 | D. | $\frac{x}{x-1}=\frac{1}{x-1}$ |
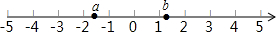 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.